 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема 3 Дифференциальные уравнения
Понятие о дифференциальных уравнениях. Общее и частное решения. Задача Коши. Дифференциальные уравнения первого порядка (неполные, с разделяющимися переменными, однородные и линейные). Уравнения, допускающие понижения порядка. Линейные уравнения n-го порядка с постоянными коэффициентами.
Студентам необходимо усвоить определение дифференциального уравнения – как уравнения, которое связывает искомую функцию одной или нескольких переменных и производные различных порядков данной функции.
Дифференциальные уравнения от одной переменной называется обыкновенными дифференциальными уравнениями, дифференциальные уравнения от нескольких переменных – дифференциальные уравнения в частных производных.
Порядок дифференциального уравнения равен порядку старшей степени производной xy¢¢¢-xy¢+5=0 – уравнение третьего порядка.
Нужно помнить, что задача интегрирования дифференциального уравнения – это задача нахождения искомого решения, а график решения называется интегральной кривой.
Общее решение обыкновенного дифференциального уравнения n-го порядка – это функция от переменных х и n произвольных независимых постоянных С1, С2, С0…,Сn.
Частное решение дифференциального уравнения – это решение, полученное из общего при некоторых значениях постоянных.
Для ряда типов дифференциальных уравнений нужно знать студенту основные понятия, нужно уметь решать однородные дифференциальные уравнения, линейные дифференциальные уравнения, неполные дифференциальные уравнения и дифференциальные уравнения с разделяющимися переменными.
Таблица соотношения начальной буквы фамилии студента и варианта контрольных заданий
| Начальная буква фамилии | Вариант задания |
| А, Е, Л | Первый |
| Р, Х, Э | Второй |
| Б, Ж, М | Третий |
| С, Ц, Ю | Четвертый |
| В, З, Н | Пятый |
| Т, Ч | Шестой |
| Г, И, О | Седьмой |
| П, У, Ш | Восьмой |
| Д, Щ, | Девятый |
| Ф, К, Я | Десятый |
ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ
ВАРИАНТ №1
Задание №1 Вычислить пределы:
а)  ; б)
; б) 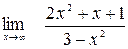 ; в)
; в) 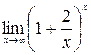
Задание №2 Найти производные функций:а) 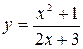 ; б)
; б) 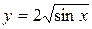 .
.
Задание №3 Исследовать функцию и построить график: у = 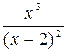 .
.
Задание №4 Найти экстремумы функций двух переменных
z = 2x3 + 6xy2 – 30x – 24y.
Задание № 5. Найти неопределенные интегралы:
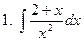
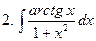

Задание № 6. Найти определенные интегралы:
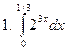
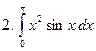

Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:

Задание № 8. Решить дифференциальное уравнение первого порядка:
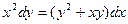
Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:

ВАРИАНТ №2
Задание №1 Вычислить пределы: а)  ; б)
; б)  ;
;
в) 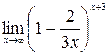
Задание №2 Найти производные функций: а) 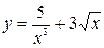 ; б)
; б) 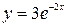 .
.
Задание№3 Исследовать функцию и построить график:  .
.
Задание №4 Найти экстремумы функций двух переменных
z = x3 – y3.
Задание № 5. Найти неопределенные интегралы:
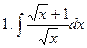
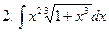

Задание № 6. Найти определенные интегралы:
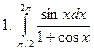

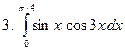
Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:
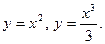
Задание № 8. Решить дифференциальное уравнение первого порядка:

Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:

ВАРИАНТ №3
Задание №1 Вычислить пределы: а) 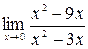 ; б)
; б)  ;
;
в) 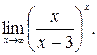
Задание №2 Найти производные функций: а) 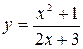 ; б)
; б) 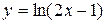 .
.
Задание№3 Исследовать функцию и построить график: 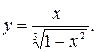
Задание №4 Найти экстремумы функций двух переменных
z = 6x2у + 2у3 – 24х – 30у.
Задание № 5. Найти неопределенные интегралы:
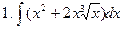


Задание № 6. Найти определенные интегралы:


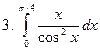
Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:
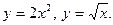
Задание № 8. Решить дифференциальное уравнение первого порядка:

Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:
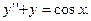
ВАРИАНТ №4
Задание №1 Вычислить пределы: а)  ; б)
; б) 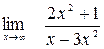 ;
;
в) 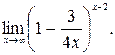
Задание №2 Найти производные функций: а)  ; б)
; б) 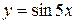
Задание№3 Исследовать функцию и построить график: 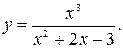
Задание №4 Найти экстремумы функций двух переменных
z = x3 – 8у3 – 6ху + 1.
Задание № 5. Найти неопределенные интегралы:
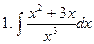
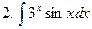

Задание № 6. Найти определенные интегралы:
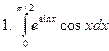
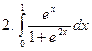
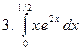
Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:
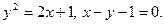
Задание № 8. Решить дифференциальное уравнение первого порядка:
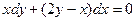
Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:
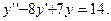
ВАРИАНТ №5
Задание №1 Вычислить пределы: а) 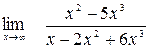 ; б)
; б) 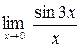 ;
;
в) 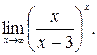
Задание №2 Найти производные функций: а) 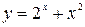 ; б)
; б) 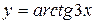
Задание№3 Исследовать и построить график: 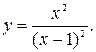
Задание №4 Найти экстремумы функций двух переменных
z = x3 – ху2 + 3х2 + у2 – 1.
Задание № 5. Найти неопределенные интегралы:
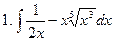

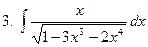
Задание № 6. Найти определенные интегралы:

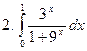

Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:

Задание № 8. Решить дифференциальное уравнение первого порядка:
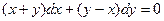
Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:
ВАРИАНТ №6
Задание №1 Вычислить пределы: а) 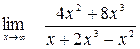 ; б)
; б) 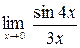 ;
;
в) 
Задание №2 Найти производные функций:а) 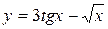 ; б)
; б) 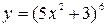 .
.
Задание№3 Исследовать функцию и построить график: 
Задание №4 Найти экстремумы функций двух переменных
z = x2у –  у3 + 2х2 + 3у2 – 1.
у3 + 2х2 + 3у2 – 1.
Задание № 5. Найти неопределенные интегралы:


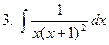
Задание № 6. Найти определенные интегралы:
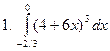
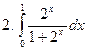
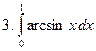
Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:
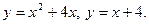
Задание № 8. Решить дифференциальное уравнение первого порядка:
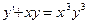
Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:
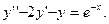
ВАРИАНТ №7
Задание №1 Вычислить пределы: а) 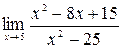 ; б)
; б) 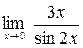 ;
;
в) 
Задание №2 Найти производные функций: а) 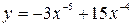 ; б)
; б) 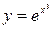 .
.
Задание №3 Исследовать функцию и построить график: 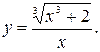
Задание №4 Найти экстремумы функций двух переменных
z = x3 + 6ху + 3у2 – 18х – 18у.
Задание № 5. Найти неопределенные интегралы:
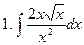
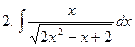
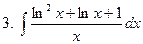
Задание № 6. Найти определенные интегралы:
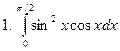
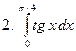
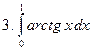
Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:

Задание № 8. Решить дифференциальное уравнение первого порядка:
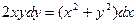
Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:
ВАРИАНТ №8
Задание №1 Вычислить пределы: а) 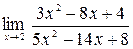 ; б)
; б) 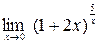 ;
;
в) 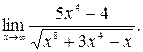
Задание №2 Найти производные функций: а)  ;
;
б)  .
.
Задание№3 Исследовать функцию и построить график: 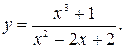
Задание №4 Найти экстремумы функций двух переменных
z = x2у – у3 – х2 – 3у2 +3.
Задание № 5. Найти неопределенные интегралы:

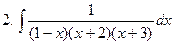
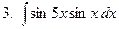
Задание № 6. Найти определенные интегралы:
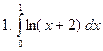
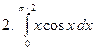

Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:
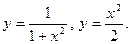
Задание № 8. Решить дифференциальное уравнение первого порядка:
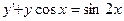
Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:
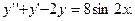
ВАРИАНТ №9
Задание №1 Вычислить пределы: а)  ; б)
; б) 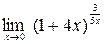 ;
;
в) 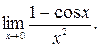
Задание №2 Найти производные функций: а) 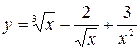 ;
;
б) 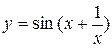 .
.
Задание№3 Исследовать функцию и построить график: 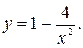
Задание №4 Найти экстремумы функций двух переменных
z = 3x2 – 6ху – у3 – 12х + 12у.
Задание № 5. Найти неопределенные интегралы:

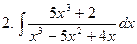
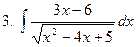
Задание №6. Найти определенные интегралы:
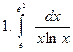


Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:
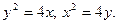
Задание № 8. Решить дифференциальное уравнение первого порядка:

Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:
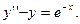
ВАРИАНТ №10
Задание №1 Вычислить пределы: а) 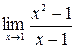 ; б)
; б) 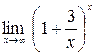 ;
;
в) 
Задание №2 Найти производные функций: а) 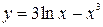 ; б)
; б) 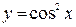 .
.
Задание№3 Исследовать функцию и построить график:  .
.
Задание №4 Найти экстремумы функций двух переменных
z = 2x3 – ху2 + 5х2 + у2.
Задание № 5. Найти неопределенные интегралы:

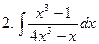

Задание № 6. Найти определенные интегралы:

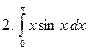
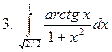
Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:

Задание № 8. Решить дифференциальное уравнение первого порядка:
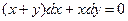
Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:

РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ
Основная литература:
1. Белова, Т.И. Вычисление неопределенных интегралов. Обыкновенные дифференциальные уравнения. Компьютерный курс: учеб. пособие / Т.И.Белова, А.А.Грешилов, И.В.Дубограй; Ред. А.А.Грешилов. - М.: Логос, 2004. - 184 с. + 1 эл. опт. диск (CD-ROM).
2. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. - 22-е изд., перераб. - СПб.: Профессия, 2006. - 432 с.
3. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. - 22-е изд., перераб. - СПб.: Профессия, 2005. - 432 с.
4. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. для вузов. В 2 ч. Ч.1 / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий. - 4-е изд., стереотип. - М.: Дрофа, 2004. - 725 с.
5. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч. 1. Дифференциальное и интегральное исчисление / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; Ред. В.А.Садовничий. - 3-е изд., испр. - М.: ДРОФА, 2001. - 725 с.
6. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч.2. Ряды, несобственные интегралы, ряды Фурье, преобразование Фурье / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; ред. В.А.Садовничий. - 3-е изд., испр. - М.: ДРОФА, 2001. - 712 с.
7. Голоскоков, Д.П. Уравнения математической физики. Решение задач в системе Maple: учеб. для вузов / Д.П.Голоскоков. - СПб.: Питер, 2004. - 538с.
8. Гурова, З.И. Математический анализ. Начальный курс с примерами и задачами: учеб. для втузов / З.И.Гурова, С.Н.Каролинская, А.П.Осипова; Ред. А.И.Кибзун. - М.: Физматлит, 2002. - 351 с.
9. Лукьянов, А.В. Обыкновенные дифференциальные уравнения: учеб. пособие по решению задач / А.В.Лукьянов, Ю.Д.Погуляев. - Челябинск: Полиграф-Мастер, 2006.
10. Математический анализ в вопросах и задачах: учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, Г.Н.Медведев, А.А.Шишкин; Ред. В.Ф.Бутузов. - 5-е изд., испр. - М.: ФИЗМАТЛИТ, 2002. - 479 с.
11. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учеб. для втузов. В 2 т. Т. 1 / Н.С.Пискунов. - Стер. изд. - М.: ИНТЕГРАЛ-ПРЕСС, 2004. - 415 с.
12. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учебник для втузов. В 2 т. Т. 2 / Н.С.Пискунов. - Стер. изд. - М.: ИНТЕГРАЛ-ПРЕСС, 2004. - 544 с.
13. Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления: учеб. для вузов. В 3 т. Т. 3 / Г.М. Фихтенгольц. - 8-е изд. - М.: ФИЗМАТЛИТ, 2003. - 727 с.
14. Фихтенгольц, Г.М. Основы математического анализа: учебник для вузов. Ч. 1 / Г.М. Фихтенгольц. - 6-е изд., стер. - СПб. Лань, 2005. - 440 с. - Алф. указ.: С. 434-440.
15. Фихтенгольц, Г.М. Основы математического анализа: учебник для вузов. Ч. 2 / Г.М.Фихтенгольц. - 6-е изд., стер. - СПб.: Лань, 2005. - 463 с.
16. Фихтенгольц, Г.М. Основы математического анализа: учебник. Ч. 1 / Г. М. Фихтенгольц. - 8-е изд. стер. - СПб.; М.; Краснодар: Лань, 2006. - 440 с.
17. Фихтенгольц, Г.М. Основы математического анализа: учебник. Ч. 2 / Г. М.Фихтенгольц. - 8-е изд. стер. - СПб.; М.; Краснодар: Лань, 2006. - 463 с.
18. Шипачев, В.С. Математический анализ: учеб. пособие для вузов / В.С.Шипачев. - М.: Высш. шк., 2002. - 176 с.
Дополнительная литература:
1. Босс, В. Лекции по математике: анализ. / В.Босс – М.: Едиториал УРСС, 2004 – 213с.
2. Босс, В. Лекции по математике: дифференциальные уравнения. / В.Босс– М.: Едиториал УРСС, 2004 – 204 с.
3. Васильева, А.Б. Интегральные уравнения / А.Б.Васильева, Н.А.Тихонов. - 2-е изд. - М.: ФИЗМАТЛИТ, 2004. – 175с.
4. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2 / П.Е.Данко [и др.]. - 7-е изд., испр. - М.: Оникс: Мир и Образование(М.), 2008. - 448 с.
5. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2 / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова, С.П.Данко. - 6-е изд. - М.: Оникс: Мир и Образование(М.), 2007. - 416 с.
6. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2-х ч. Ч.2 / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. - 6-е изд. - М.: Оникс: Мир и Образование(М.), 2005. - 416 с.
7. Задачи и упражнения по математическому анализу для втузов / Ред. Б.П.Демидович. – М.: АСТ-Астрель, 2004. - 495 с.
8. Зайцев, В.Ф. Справочник по обыкновенным дифференциальным уравнениям / В.Ф.Зайцев, А.Д.Полянин. - М.: Физматлит, 2001. - 576 с.
9. Краснов, М.Л., Интегральные уравнения. Задачи и примеры с подробными решениями: учеб.пособие. / М.Л.Краснов, А.И.Киселев, Г.И. Крамаренко – М.: Едиториал УРСС, 2003 – 192с.
10. Кудрявцев, Л.Д. Краткий курс математического анализа: учеб. для вузов. В 2 т. Т. 1 Дифференциальное и интегральное исчисления функции одной переменной. Ряды / Л.Д.Кудрявцев. - 2-е изд., перераб. и доп. - Висагинас: Alfa, 1998. - 397 с.
11. Математический анализ и линейная алгебра. Учебное–методическое пособие. / Под ред. Н.Ш.Кремера. – М.: ВЗФЭИ, 2002.
12. Сборник задач и упражнений по математическому анализу. Ч.1 / С.И.Ляшко [и др.]; Ред. И.И. Ляшко. - М.; СПб.; Киев: Диалектика, 2001. - 430 с.
13. Стакун, А.А. Математический анализ: конспект лекций с решениями типовых примеров и метод. указ. к инд. заданиям (для студ.-заоч.). В 2 ч. Ч.2 / А.А.Стакун, С.И.Фролов. - СПб.: Политехника, 2001. - 147 с.
Приложение 1
Таблица производных и интегралов

Приложение 2
Поиск по сайту: