 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Связь интенсивности раздражителя с характеристиками потенциалов действия. Функции сжатия. Отображение качественных характеристик раздражителей
Сигналы одной модальности могут различаться по силе (точнее – по интенсивности). В какой же характеристике потенциалов действия отображаются эти различия? Нетрудно понять, что в соответствии с законом «всё или ничего» все потенциалы действия в данном нервном волокне одинаковы, поэтому величина (амплитуда) и форма ПД не могут служить сигнальными признаками для различения сильных и слабых раздражителей. Эксперименты показали, что от интенсивности раздражителя зависит частота следования потенциалов действия в нервном волокне, отходящем от рецептора. Чем сильнее раздражитель, тем короче интервалы между потенциалами действия, и тем выше частота следования ПД.
Очень важно, что зависимость следования ПД от интенсивности раздражителя почти всегда нелинейная, то есть между частотой и интенсивностью нет прямой пропорциональности. Легко понять, что так и должно быть, потому что интенсивность большинства раздражителей может меняться в очень широких пределах. Например, интенсивность самого громкого звука, ещё не повреждающего орган слуха, больше интенсивности самого тихого (порогового) звука в 1014 раз! Ясно, что частота нервных импульсов (потенциалов действия) не может измениться в такое колоссальное число раз. Между частотой и интенсивностью должна существовать нелинейная функциональная зависимость, при которой интервал частот сжат во много раз по сравнению с интервалом интенсивностей. Такую функцию так и называют – функция сжатия.
Во многих случаях функция сжатия близка к логарифмической функции: 
,
где ν – частота следования ПД, I – интенсивность раздражителя, Iо – пороговая интенсивность (минимальная ощущаемая интенсивность раздражителя), k – коэффициент, зависящий от других характеристик раздражителя (кроме интенсивности), а также от выбора единиц измерения. (Эта формула называется законом Вебера – Фехнера). Легко видеть, что логарифмическая функция – это очень эффективная функция сжатия. Например, если интенсивность раздражителя возрастёт в 1010 раз (колоссальное число!), частота ПД увеличится только на 10k единиц (lg 1010 = 10). Так как коэффициент k обычно не очень велик, изменение частоты составит десятки, максимум – сотни герц, что очень мало по сравнению с изменением интенсивности.
Другое важное свойство логарифмической функции легко получить, если взять производную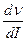 
: dν/dI = k(lgI - lgI0)΄ = k.(1/I) или dν = k(dI/I).
Отсюда видно, что абсолютное изменение частоты пропорционально относительному изменению интенсивности. Но именно такое соотношение гарантирует наиболее целесообразную точность восприятия интенсивности: при больших интенсивностях нет надобности оценивать интенсивность с малой абсолютной ошибкой. Понятно, что при покупке на 10 рублей разница в 1 рубль (10%) достаточно существенна, но вряд ли кто-нибудь обратит внимание на такую разницу, покупая машину за 100 000 р. (она составит 0,001%). Другими словами, при оценке интенсивности раздражителя практически значимы не абсолютные, а относительные величины; именно это и обеспечивает логарифмическая функция.
Другим вариантом функции сжатия может быть степенная зависимость:
ν = k.In,
где показатель степени n < 1 (то есть, другими словами, величина I стоит под корнем). Например, если n = 0,2 (корень пятой степени), то при изменении интенсивности в 1010 раз частота изменится в (1010)0,2 = 100,2.10 = 100 раз, то есть опять таки изменение частоты много меньше изменения интенсивности.
Надо заметить, что из-за большой сложности биофизических процессов в сенсорных системах никакая простая математическая функция не может в точности отобразить связь частоты нервных импульсов с интенсивностью раздражителя. Особенно большие отклонения наблюдаются при очень малых или при очень больших интенсивностях. Однако, в области средних интенсивностей (которые на практике встречаются чаще всего) логарифмическая или степенная функции достаточно хорошо отображают результаты, получаемые в эксперименте или при клиническом обследовании.
Другой способ получения информации об интенсивности раздражителясвязан с тем, что почти всегда эта информация передаётся не от одного изолированного рецептора, а от большого их числа по многим волокнам. Порог возбуждения у разных рецепторов различен, поэтому чем больше интенсивность раздражителя, тем больше рецепторов участвует в передаче сигнала, и тем больше клеток в нервных центрах будет возбуждено. Связь между интенсивностью раздражителя и возбуждением нервных центров тоже нелинейная; есть данные, что здесь лучше подходит степенная функция. Однако, этот вопрос пока недостаточно изучен.
Поиск по сайту: