Тема 8. Экономический рост

1. Предпосылки и характерные черты современного экономического роста.

Под экономическим ростом понимают увеличение реального дохода в экономике (ВНП, ВВП или НД), а также рост реального выпуска в расчете на душу населения. Соот­ветственно, для измерения экономического роста используют­ся показатели абсолютного прироста или темпов прироста ре­ального объёма выпуска в целом или на душу населения.

2. Источники экономического роста.

Экономический рост называется экстенсивным, если он осуществляется за счет привлечения дополнительных ресурсов и не меняет среднюю производительность труда в обществе. Интенсивный рост связан с применением более совершенных факторов производства и технологии, т.е. осуществляется не за счет увеличения объемов затрат ресурсов, а за счет роста их отдачи. Интенсивный рост может служить основой повыше­ния благосостояния населения. Обычно говорят о преимуще­ственно интенсивном или экстенсивном типе экономического роста в зависимости от удельного веса тех или иных факторов, вызвавших этот рост.

К экстенсивным факторам относят рост затрат капитала, труда, к интенсив­ным — технологический прогресс, экономию на масштабах, рост образовательного и профессионального уровня работни­ков, повышение мобильности и улучшение распределения ре­сурсов, совершенствование управления производством, соот­ветствующее улучшение законодательства и тд., т.е. всё, что позволяет качественно усовершенствовать как сами факторы производства, так и процесс их использования. Иногда в виде самостоятельного фактора экономического роста выделяют совокупный спрос как главный катализатор процесса расши­рения производства.

В качестве причин, сдерживающих экономический рост, часто называют ресурсные и экологические ограничения, ши­рокий спектр социальных издержек, связанных с ростом про­изводства, а также неэффективную экономическую политику правительства.

3. Факторная модель роста.

Большинство моделей роста исходит из того, что увеличение реального объема выпуска происходит, прежде всего, под влиянием роста основных факторов производства — труда (L) и капитала (К).

Наиболее простой кейнсианской моделью роста является модель Е.Домара, предложенная в конце 1940-х годов. Технология производства представлена в ней производственной функцией Леонтьева с постоянной предельной производительностью капитала (при условии, что труд не является дефицитным ресурсом). Модель Домара исходит из того, что на рынке труда существует избыточное предложение, что обусловливает постоянство уровня цен. Выбытие капитала отсутствует, отношение К/Y и норма сбережений - постоянны. Выпуск зависит фактически от одного ресурса - капитала. Для простоты можно принять также инвестиционный лаг равным нулю.

Фактором увеличения спроса и предложения в экономике служит прирост инвестиций.

Равновесный экономический рост будет достигнут при условии равенства спроса и предложения, т.е. темп прироста инвестиции должен быть равен произведению предельной производительности капитала и предельной склонности к сбережению.

Согласно теории Е. Домара, существует равновесный темп прироста реального дохода в экономике, при котором полностью используются имеющиеся производствен­ные мощности. Он прямо пропорционален норме сбережений и предельной производительности капитала, или приростной капиталоотдаче, . Инвестиции и доход растут с одинаковым постоянным во времени темпом.

Р.Ф. Харрод построил специальную модель экономиче­ского роста (1939г.), включив в неё эндогенную функцию ин­вестиций (в отличие от экзогенно заданных инвестиций у Домара) на основе принципа акселератора и ожиданий предпри­нимателей.

Согласно принципу акселератора, любой рост (сокращение) дохода вызывает рост (сокращение) капитало­вложений, пропорциональный изменению дохода.

По Харроду "гарантированный» темп роста: поддерживая его, предприниматели будут полностью удовле­творены своими решениями, поскольку спрос будет равен предложению и их ожидания будут сбываться. Такой темп рос­та обеспечивает полное использование производственных мощностей (капитала), но полная занятость при этом не все­гда достигается.

Помимо гарантированного темпа роста Харрод вводит по­нятие "естественного" темпа роста. Это максимальный темп, допускаемый ростом активного населения и техническим прогрессом.

Технический прогресс в модели Харрода не меняет соотношений

При таком темпе достигается полная занятость факторов - труда и капитала.

Если гарантированный темп роста, удовлетворяющий предпринимателей, выше естественного, то вследствие недостатка трудовых ресурсов фактический темп окажется ниже га­рантированного: производители будут разочаровываться в сво­их ожиданиях, снизят объём выпуска и инвестиции, в резуль­тате чего система будет находиться в состоянии депрессии.

Если гарантированный темп роста меньше естественного, то фактический темп может превысить гарантированный, поскольку существующий избыток трудовых ресурсов даёт возможность уве­личить инвестиции. Экономическая система будет переживать бум. Фактический темп роста может быть также равен гарантиро­ванному, и тогда экономика будет развиваться в условиях дина­мического равновесия, вполне удовлетворяющих предпринимате­лей, но при наличии вынужденной безработицы.

Идеальное развитие экономической системы достигается при равенстве гарантированного, естественного и фактиче­ского темпов роста в условиях полной занятости ресурсов.

Но поскольку всякое отклонение инвестиций от условий га­рантированного темпа роста, как известно, выводит систему из равновесия и сопровождается всё более увеличивающимся расхо­ждением между спросом и предложением, динамическое равно­весие в модели Харрода также оказывается неустойчивым.

Часто обе модели объединяют в одну модель Харрода-Домара. Обе модели приводят к выводу, что при данных тех­нических условиях производства темп экономического роста определяется величиной предельной склонности к сбереже­нию, а динамическое равновесие может существовать в усло­виях неполной занятости.

4. Модель Солоу долгосрочного роста.

Р.Солоу показал, что нестабильность динамического равновесия в кейнсианских моделях была следствием невзаимо­заменяемости факторов производства. Вместо функции Леонтьева он использовал в своей модели производственную функцию Кобба—Дугласа, в которой труд и капитал являются суб­ститутами. Другими предпосылками анализа в модели Солоу являются: убывающая предельная производительность капита­ла, постоянная отдача от масштаба, постоянная норма выбы­тия, отсутствие инвестиционных лагов.

Взаимозаменяемость факторов (изменение капиталовооруженности) объясняется не только технологическими усло­виями, но и неоклассической предпосылкой о совершенной конкуренции на рынках факторов.

Необходимым условием равновесия экономической сис­темы является равенство совокупного спроса и предложения. Предложение описывается производственной функцией с по­стоянной отдачей от масштаба: Y =F(K,L) и для любого поло­жительного z верно; zF(K,L) = F (zK, zL). Тогда если z=1/L, то 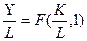. Обозначим через y, а через k и перепишем исходную функцию в форме взаимосвязи между произ­водительностью и фондовооруженностью (капиталовооружен­ностью): y=f(k). Тангенс угла наклона данной производственной функции соответствует предельному про­дукту капитала (МРК), который убывает по мере роста фондо­вооруженности (k).

Совокупный спрос в модели Солоу определяется инвести­циями и потреблением: y=i+c, где i и с - инвестиции и по­требление в расчете на одного занятого. Доход делится между потреблением и сбережениями в соответствии с нормой сбе­режения, так что потребление можно представить как c=(l - s)y, где s - норма сбережения (накопления), тогда y=c+i=(l-s)y+i, откуда i=sy. В условиях равновесия инвестиции рав­ны сбережениям¹ и пропорциональны доходу.

Условия равенства спроса и предложения могут быть представлены как ƒ(k)=c+i или ƒ = (k)= . Производственная функция определяет предложение на рынке товаров, а накоп­ление капитала - спрос на произведенный продукт.

Динамика объёма выпуска зависит от объёма капитала (в нашем случае - капитала в расчете на одного занятого, или капиталовооруженности). Объём капитала меняется под воз­действием инвестиций и выбытия: инвестиции увеличивают запас капитала, выбытие - уменьшает.

Инвестиции зависят от фондовооруженности и нормы на­копления, что следует из условия равенства спроса и предло­жения в экономике; i=s·ƒ(k). Норма накопления определяет деление продукта на инвестиции и потребление при любом значении k (рис. 12,1): y=ƒ(k), I=s·ƒ(k), c=(1-s)·ƒ(k).

Амортизация учитывается следующим образом: если при­нять, что ежегодно вследствие износа капитала выбывает его фиксированная часть d (норма выбытия), то величина выбы­тия будет пропорциональна объёму капитала и равна d·k. На графике эта связь отражается прямой, выходящей из точки начала координат, с угловым коэффициентом d.

Влияние инвестиций и выбытия на динамику запасов ка­питала можно представить уравнением: Δk = i – dk, или, используя равенство инвестиций и сбережений, Δk= s • ƒ(k) - dk. Запас капитала (k) будет увеличиваться (Δk>0) до уровня, при котором инвестиции будут равны вели­чине выбытия, т.е. s·ƒ(k)=dk. После этого запас капитала на одного занятого (фондовооруженность) не будет меняться во времени, поскольку две действующие на него силы уравновесят друг друга (Δk=0). Уровень запаса капитала, при котором инвестиции равны выбытию, называется равновесным (устойчивым) уровнем фондовооруженности труда и обозначается k*. При достижении k* экономика находится в состоянии долгосрочного равновесия.

Равновесие является устойчивым, поскольку независимо от исходного значения k экономика будет стремиться к равно­весному состоянию, т.е. к k*. Если начальное k₁ ниже k*, то валовые инвестиции (s•ƒ(k)) будут больше выбытия (dk) и запас капитала будет возрастать на величину чистых инвестиций. Если k₂ > k*, это означает, что инвестиции меньше, чем износ, а значит запас капитала будет сокращаться, приближаясь к уровню k*.

Норма накопления (сбережения) непосредственно влияет на устойчивый уровень фондовооруженности. Рост нормы сбережения с s₁ до s₂ сдвигает кривую инвестиций вверх из положения s₁ ƒ(k) до s₂ (k).

В исходном состоянии экономика имела устойчивый запас ка­питала k₁*, при котором инвестиции равнялись выбытию. По­сле повышения нормы сбережения инвестиции выросли на (i^/₁-i₁), а запас капитала (k₁*) и выбытие (dk₁) остались прежними. В этих условиях инвестиции начинают превышать выбытие, что вызывает рост запаса капитала до уровня нового равновесия k₂*, которое характеризуется более высокими зна­чениями фондовооруженности и производительности труда (выпуск на одного занятого, у).

Таким образом, чем выше норма сбережения (накопления), тем более высокий уровень выпуска и запаса капитала может быть достигнут в состоянии устойчивого рав­новесия. Однако повышение нормы накопления ведёт к уско­рению экономического роста в краткосрочном периоде, до тех пор, пока экономика не достигнет точки нового устойчивого равновесия.

Очевидно, что ни сам процесс накопления, ни увеличение нормы сбережения не могут объяснить механизм непрерыв­ного экономического роста. Они показывают лишь переход от одного состояния равновесия к другому.

Для дальнейшего развития модели Солоу поочередно снимаются две предпосылки; неизменность численности насе­ления и его занятой части (их динамика предполагается оди­наковой) и отсутствие технического прогресса.

Предположим, население растёт с постоянным темпом п. Это новый фактор, влияющий вместе с инвестициями и выбы­тием на фондовооруженность. Теперь уравнение, показываю­щее изменение запаса капитала на одного работника, будет выглядеть как: Δk=i-dk-nk или Δk=i-(d+n)k.

Рост населения аналогично выбытию снижает фондово­оруженность, хотя и по-другому - не через уменьшение на­личного запаса капитала, а путем распределения его между возросшим числом занятых. В данных условиях необходим та­кой объем инвестиций, который не только бы покрыл выбы­тие капитала, но и позволил бы обеспечить капиталом новых рабочих в прежнем объеме. Произведение nk показывает, сколько требуется дополнительного капитала в расчете на од­ного занятого, чтобы капиталовооруженность новых рабочих была на том же уровне, что и старых.

Условие устойчивого равновесия в экономике при неиз-фондовооруженности k* можно будет записать теперь

∆k=s•ƒ(k)-(d+n)k=0 или s•ƒ(k)=(d+n)k

Данное состояние характеризуется полной занятостью ре­сурсов.

В устойчивом состоянии экономики капитал и выпуск на одного занятого, т.е. фондовооруженность (k) и производи­тельность (у) труда остаются неизменными. Но, чтобы фондо­вооруженность оставалась постоянной и при росте населения, капитал должен возрастать с тем же темпом, что и население, .

Изменения фондовооруженности (k), необходимое для поддержания устойчивого равновесия на уровне k*, происходит за счет гибкости цен на факторы производства. Например, при k2>k* объём капитала на одного занятого недостаточен для оснащения должным образом новой рабочей силы и покрытия выбытия. Это означает, что часть рабочей силы останется безработной. Но в условиях свободной конкуренции на рынках факторов безработица приведёт к снижению цены труда по отношению к цене капитала, и предприниматели предпочтут перейти к новой технологии, требующей больше затрат труда и меньше капитала. Таким образом фондовооруженность (k₂) снизится в направлении k*. Аналогичные рассуждения можно привести и для k₁<k*, что свидетельствует о наличии внутренних механизмов движения системы к состоянию устойчивого равновесия.

Таким образом, рост населения становится одной из при­чин непрерывного экономического роста в условиях равнове­сия.

Отметим, что с увеличением темпа роста населения воз­растает угловой коэффициент кривой (d+n)k, что приводит к уменьшению равновесного уровня фондовооруженности (k'*), а следовательно, к падению у.

Учет в модели Солоу технологического прогресса видоиз­меняет исходную производственную функцию. Предполагается трудосберегающая форма технологического прогресса. Произ­водственная функция будет представлена как Y=F(K,L•E), где Е - эффективность труда, a (L•E) - численность условных единиц труда с постоянной эффективностью Е. Чем выше Е, тем больше продукции может быть произведено данным чис­лом работников. Предлагается, что технологический прогресс осуществляется путем роста эффективности труда Е с посто­янным темпом g. Рост эффективности труда в данном случае аналогичен по результатам росту численности занятых: если технологический прогресс имеет темп g=2%, то, например, 100 рабочих могут произвести столько же продукции, сколько ра­нее производили 102 рабочих. Если теперь численность заня­тых (L) растет с темпом л, а Е растет с темпом g, то (L•E) бу­дет увеличиваться с темпом (n+g).

Включение технологического прогресса несколько меняет и анализ состояния устойчивого равновесия, хотя ход рассуж­дений сохраняется. Если определить k’ как количество капита­ла в расчете на единицу труда с постоянной эффективностью, т.е. k’ = 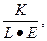а y’ = , то результаты роста эффективных единиц труда аналогичны росту численности занятых (увеличение количества единиц труда с постоянной эффектив­ностью снижает величину капитала, приходящегося на одну такую единицу). В состоянии устойчивого равновесия (рис. 12.5) уровень фондовооруженности k'* уравновешивает, с од­ной стороны, влияние инвестиций, повышающих фондово­оруженность, а, с другой стороны, воздействие выбытия, роста числа занятых и технологического прогресса, снижающих уро­вень капитала в расчете на эффективную единицу труда:

s•ƒ(k’)=(d+n+g)k’.

В устойчивом состоянии (k'*) при наличии технологиче-го прогресса общий объём капитала (К) и выпуска (Y), бу-расти с темпом (n+g). Но в отличие от случая роста насе-ния, теперь будут расти с темпом g фондовооруженность 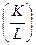- и выпуск b расчете на одного занятого; последнее может служить основой для повышения благосостояния населения. Технологический прогресс в модели Солоу является, следовательно, единственным условием непрерывного роста уровня жизни, поскольку лишь при его наличии наблюдается устойчивый рост выпуска на душу населения (у).

Поиск по сайту: