 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Принцип решения СЛУ методом Зейделя
Метод Зейделя можно считать усовершенствованным методом простых итераций. При решении системы методом итерации каждый шаг итерационного процесса состоит в переходе от уже имеющегося приближения значений неизвестных к новому (очередному) приближению. Основная идея метода Зейделя состоит в том, что на каждом шаге итерационного процесса учитываются уже полученные значения.
Если обозначить через х 1, х 2, …, х n элементы имеющегося приближения, а элементы очередного приближения через y 1, y 2. …, y n, то вычислительная формула для метода простой итерации имеет вид
 (i = 1, 2, …, n).
(i = 1, 2, …, n).
Соответствующие вычислительные формулы для метода Зейделя:


………………………….
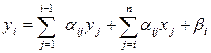
…………………………..
 .
.
Справедливо следующее утверждение: если для матрицы коэффициентов приведенной системы выполняется хотя бы одно из условий сходимости, то итерационный процесс метода Зейделя сходится к решению системы при любом выборе начального приближения.
Таким образом, каждое из трех условий сходимости является достаточным для итерационного процесса метода Зейделя. Преимущество этого метода состоит в том, что он обычно обеспечивает более быструю сходимость, чем метод простой итерации.
Рассмотрим метод на конкретном примере, использованном ранее.
Решим систему трех линейных уравнений с тремя неизвестными с точностью e = 10-4.
2,34 х 1 – 4,21 х 2 – 11,61 х 3 = 14,41
8,04 х 1 + 5,22 х 2 + 0,27 х 3 = -6,44
3,92 х 1 – 7,99 х 2 + 8,37 х 3 = 55,56
Приведенная система имеет вид:
х 1= - 0,649 х 2 - 0,0,34 х 3 - 0,801
х 2 = - 0,513 х 1 – 0,266 х 3 – 5,735
х 3 = 0,202 х 1 – 0,363 х 2 – 1,241.
Ранее было показано, что процесс сходится в пространстве с евклидовой метрикой.
В качестве начального приближения примем столбец свободных членов:
х 1(0) = -0,801; х 2(0) = -5,735; х 3(0) = -1,241.
Рассмотрим, как выполняется первая итерация Зейделя:
х 1(1) = -0,649 х 2(0) -0,034 х 3(0) – 0,801 =
= -0,649 (-5,735) – 0,034 (-1,241) – 0,801 = 2,9632.
Далее, при вычислении х 2(1) используется уже найденное только что значение х 1(1):
х 2(1) = 0,513 х 1(1) - 0,266 х 3(0) – 5,735 =
= 0,513 × 2,9632 - 0,266 (-1,241) – 5,735 = -3,8848.
Аналогично, при вычислении х 3(1) используются уже найденное только что значения х 1(1) и х 2(1):
х 3(1) = 0,202 х 1(1) - 0,363 х 2(1) – 1,241 =
= 0,202 × 2,9632 - 0,363 (-3,8848) – 1,241 = 0,7678.
Итак, получено первое приближение решения системы. Итерации продолжаются подобным образом до получения заданной точности.
Поиск по сайту: