Решение системы линейных уравнений с помощью математического пакета Mathcad

Mathcad — программа для выполнения и документирования инженерных и научных расчётов.

Основные возможности Mathcad:

- решение дифференциальных уравнений различными численными методами;

- построение двух- и трёхмерных графиков функций;

- использование греческого алфавита как в уравнениях, так и в тексте;

- выполнение вычислений в символьном режиме;

- выполнение операций с векторами и матрицами;

- символьное решение систем уравнений;

- аппроксимация кривых;

- выполнение подпрограмм;

- поиск корней многочленов и функций;

- проведение статистических расчётов и работа с распределением вероятностей;

- поиск собственных чисел и векторов;

- вычисления с единицами измерения;

- интеграция с САПР системами, использование результатов вычислений в качестве управляющих параметров.

Некоторые правила работы для начинающих:

§ Выражения, тексты (комментарии), любые другие объекты могут располагаться в любом месте рабочего поля; работать с ними как с единым объектом можно аналогично графическим объектам: выделять, копировать, перемещать, форматировать и др. Удаление, добавление пустых строк – такое же, как в любом текстовом редакторе.

§ Если в целях наглядности необходим текстовый комментарий, то предварительно, воспользовавшись клавишей <”>, следует создать текстовую область: при этом крестообразный курсор преобразуется в маркер ввода и появится текстовая рамка; после окончания печати текста нужно щелкнуть мышью за текстовой рамкой. Можно просто начать ввод теста в место расположения курсора.

§ Для ввода выражения и присвоения его значения переменной используется знак Definition «:=» панели Evaluation; при его выборе появляется шаблон . В его левую часть вводится имя переменной, в правую – выражение. При этом тип переменной (и, соответственно, выражения), как в языках программирования, не задается; это определятся по контексту. Переменная может быть, например, простой переменной вещественного типа или матрицей.

§ Для получения результата вычислений используется знак Evaluate Numerically «=» панели Evaluation. После ввода имени переменной в левую часть окончания ввода (Enter или щелчок вне объекта) появляется результат.

§ Для ввода матриц, нумерованных матриц, интервалов значений, элементарных функций и операций и т. д. используются панели Matrix и Calculator.

§ Результаты работы сохраняются в воде файлов типа Mathcad Document.

Пример использования Mathcad:

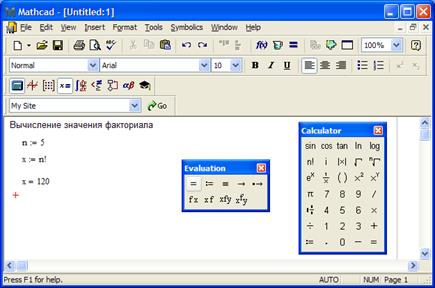
Задача: решить систему линейных уравнений методом простой итерации с точностью e =10-4.

Для решения используется преобразованная система уравнений. Сама система вводится как текст (комментарий). Замечание: для записи используется символьный знак равенства на панели Boolean или сочетанием клавиш Ctrl - =.

Для проверки достаточного условия сходимости можно использовать любую из норм, каждую их которых вычисляет своя встроенная функция:

norm1 (A) – вычисляет максимальную из сумм модулей коэффициентов при неизвестных, взятых по строкам;

normi (A) - вычисляет максимальную из сумм модулей коэффициентов при неизвестных, взятых по столбцам;

norme (A) – вычисляет сумму квадратов коэффициентов (замечание: без извлечения квадратного корня).

В качестве начального (нулевого) приближения выбирается вектор-столбец b свободных членов преобразованной системы. Количество итераций задается в пределах от 1 до 25. Для ввода векторов – приближений используется кнопка панели Matrix.

Для просмотра всех полученных приближений используются приемы, аналогичные электронным таблицам: клавиши работы с курсором или полосы прокрутки.

Решение системы:

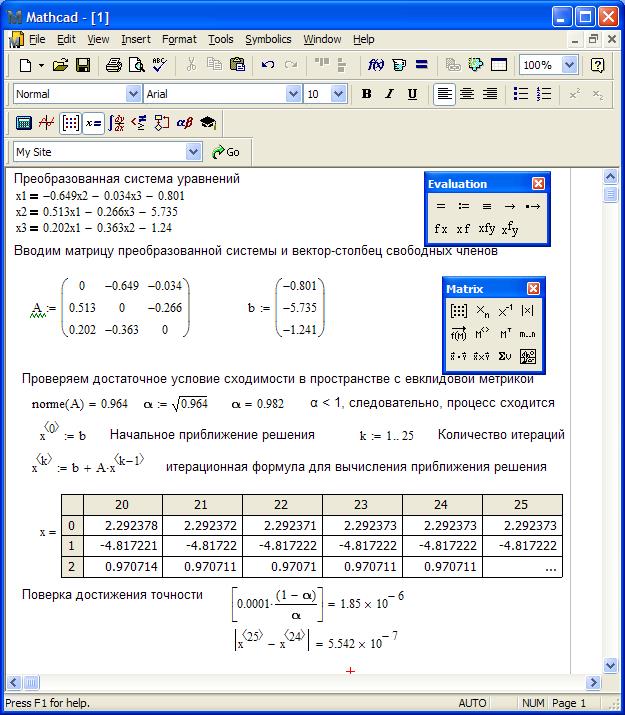
Можно проверить, что заданная точность достигается на 24-ой итерации:

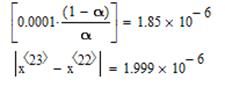
Ответ (с округлением до заданной точности):

х₁ = 2,2924, х₂ = -4,8172, х₃ = 0,9707.

Математический пакет Mathcad можно использовать и для решения СЛУ методом Зейделя.

Задача: решить систему трех линейных уравнений с тремя неизвестными с точностью e = 10-4.

2,34 х ₁ – 4,21 х ₂ – 11,61 х ₃ = 14,41

8,04 х ₁ + 5,22 х ₂ + 0,27 х ₃ = -6,44

3,92 х ₁ – 7,99 х ₂ + 8,37 х ₃ = 55,56

Приведенная система имеет вид:

х ₁= - 0,649 х ₂ - 0,0,34 х ₃ - 0,801

х ₂ = - 0,513 х ₁ – 0,266 х ₃ – 5,735

х ₃ = 0,202 х ₁ – 0,363 х ₂ – 1,241.

Метод Зейделя может быть реализован при помощи вычислительного блока Given. На рабочем листе вводится оператор Given, под которым записывается преобразованная система линейных уравнений. Затем вызывается диалоговое окно Insert Function, выбирается функция find и нажатием кнопки ОК вызывается соответствующий шаблон . Перед вызовом функции необходимо вставить символ 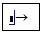из панели Evaluation. На место маркеров следует ввести имена неизвестных x ₁, x ₂, x ₃. Требуемую точность вычислительного процесса обеспечивает системная переменная TOL, вызов которой осуществляет команда Worksheet Options меню Tools.

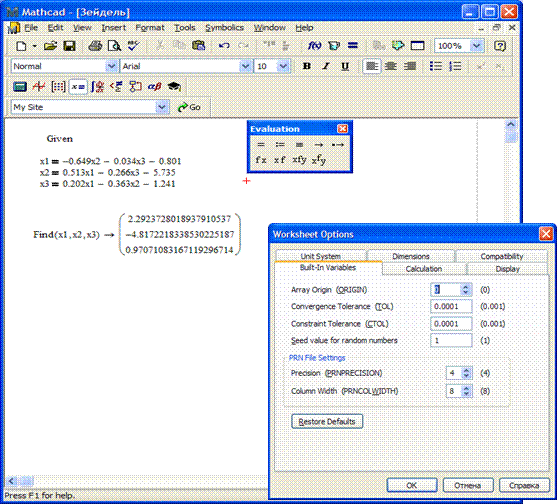
Результат с точностью до 4-х цифр, естественно, совпадает с предыдущими. К сожалению, в MathCad нельзя узнать, сколько итераций потребовалось для получения окончательного результата методом Зейделя.

Поиск по сайту: