Кейнсианские модели экономического роста

Основные современные модели роста – кейнсианские. Как и любые модели, модели роста представляют абстрактное, упрощенное выражение реального экономического процесса в форме уравнений и графиков.

Большинство моделей роста исходит из того, что увеличение реального объема выпуска происходит, прежде всего, под влиянием основных факторов производства – труда (L) и капитала (K). Фактор «труд» обычно слабо поддается воздействию извне, тогда как величина капитала может быть скорректирована определенной инвестиционной политикой.

Наиболее простой кейнсианской моделью роста является модель Е. Домара, предложенная в конце 40-х гг. Данная модель исходит из того, что на рынке труда существует избыточное предложение, что обусловливает постоянство уровня цен. Выбытие капитала отсутствует, отношение К/У и норма сбережений – постоянны. Выпуск зависит фактически от одного ресурса – капитала. Для простоты можно принять инвестиционный лаг равным нулю.

Фактором увеличения спроса и предложения в экономике служит прирост инвестиций. Если в данном периоде инвестиции выросли на Δ I, то в соответствии с эффектом мультипликатора, совокупный спрос возрастает на:

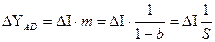Увеличение совокупного предложения составит:

ΔY_AS = a × DK, где

a - предельная производительность капитала.

Равновесный экономический рост будет достигнут при условии равенства спроса и предложения:

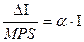
или, т.е.

темп прироста инвестиций должен быть равен произведению предельной производительности капитала и предельной склонности к сбережению. Величина a задается технологией производства и, в соответствии с принятыми предпосылками, постоянна, а, значит, увеличить темпы прироста инвестиций может лишь рост нормы сбережений s (но для рассматриваемого периода она берется постоянной).

Поскольку в условиях равновесия I = S, а S = s ×Y при s = const, уровень дохода является величиной, пропорциональной уровню инвестиций, и тогда:

Такое динамическое равновесие может оказаться неустойчивым, как только темп роста плановых инвестиций частичного сектора экономики отклоняется от уровня, заданного моделью.

Р.Ф. Харрод построил специальную модель экономического роста.

Для всех кейнсианских моделей экономического роста общей является зависимость между сбережениями и инвестициями.

Так, в рассуждениях Харрода рост своим отправным пунктом имеет инвестирование нового капитала (это есть и у Кейнса), расширение производственной мощности национальной экономики, т.е. накопление капитала.

Особую роль в выводах Харрода играют отношение и показатель «капитал-продукт».

Темп прироста национального продукта он определял как отношение нормы валовых инвестиций (которая считается равной склонности к сбережению всего общества) к показателю капитал – продукт.

Y – прирост национального продукта;

Y = S/K, S – склонность к сбережениям;

K – «капитал - продукт» (или «капитал- доход» в денежном выражении).

где Т_пр – темп прироста НД,

DНД – прирост НД,

ФН – фонд накопления,

N_Н – норма накопления в НД,

DКЁ – капиталоёмкость прироста НД.

Если обозначить DНД/ФН = Э_кв, то можно записать

- известная формула связи темпов прироста НД, нормы накопления и эффективности инвестиций.

Обозначения Харрода несколько специфичны:

G – прирост ВНП в единицу времени, выраженный в виде части всего продукта (DY/Y);

С – капитальный коэффициент, т.е. отношение между объемом капитала вложенного в производство и обеспечиваемым приростом продукта (I/DY);

I, S и Y – капитал (инвестиции), сбережения, доход.

Инвестиции нейтральны, т.е. I/DY – const, r (ставка %) - const.

Задача экономического расчета состояла в следующем: при данных величинах G и S найти требуемую величину С.

И при S = S/Y выходим на простое выражение равновесия S/Y = I/Y, или I = S.

Используя эти обозначения, Харрод вводит ряд новых понятий в теории роста:

1) G_w – гарантированный темп роста, обеспечивающий постоянный процент прироста продукции

2) C_r – требуемый капитальный коэффициент

3) S’ – склонность к сбережению

4) G_n – процент естественного прироста или необходимый темп развития.

В результате им получены 3 значения формулы роста:

1. G_w×C_r = S’ или G_w = S’/C_r

2. Gn×Cr = S Gn = S/Cr

3. Gn×Cr = Sr (равновесный уровень склонности к сбережению)

4. G_n = S_r/C_r

Последние две формулы выражают варианты не нейтрального НТП. Они показывают, что в долгосрочном периоде роста возможно как равновесное, так и неравновесное состояния.

Динамическое равновесие (оптимальный темп роста) достигается в случае, когда:

S = S_r.

Однако имеются и два случая неравновесного роста.

1. S > S_r – избыточность сбережений. В воспроизводственном процессе при такой ситуации имеет место неполная занятость и застой в экономике. Существует избыточное предложение инвестиционного капитала, и даже приемлемый уровень % не обеспечивает достаточных стимулов к новому качеству роста.

2. S < S_r – недостаточность сбережений. Экономика характеризуется индустриальной активностью предпринимателей, кредиты весьма дороги, инвестиции начинают финансироваться за счет «печатного станка», необеспеченных ценных бумаг, экономика «вползает» в хроническую инфляцию.

В литературе имеется и адаптированный к понятиям воспроизводства вариант модели Харрода – Домара, в котором несколько изменен смысл видов роста – естественного и гарантированного, а также вводится новое понятие «фактический рост». Ввиду важности указанной модели в теории роста рассмотрим кратко ее основные компоненты.

Модель Харрода – Домара предназначена для определения постоянного сбалансированного темпа роста экономики, при котором все основные компоненты экономической системы изменяются во времени с одинаковой скоростью, при полной занятости населения в трудоспособном возрасте. Основные предпосылки модели:

· экономика рассматривается в виде одной отрасли, производящей однородный и бесконечно делимый продукт;

· для производства товаров необходимы 2 вида ресурсов – труд и капитал;

· количество труда и капмтала, требуемое для сбережений, являющихся источником финансирования прироста новых мощностей, постоянна.

· отсутствует экономия затрат при увеличении масштабов производства.

В модели существуют обозначения:

Y – национальный доход;

K – чистые капиталовложения;

s – норма сбережения НД

b – удельная фондоемкость дохода (b = F/Y)

T_p – темп роста населения

T_y – темп прироста дохода

T_f – темп роста капитала.

Главная задача модели – определение устойчивого темпа роста дохода.

Для этого существуют 3 основных вида темпов роста (естественный, гарантированный, фактический).

Условием существования постоянного равновесного темпа роста экономической системы является соблюдение равенства темпов роста населения и капитала.

,

В реальной действительности соотношения T_Р и S/b могут быть таковы:

а) T_Р<S/b – в производстве полная занятость, но избыток производственных мощностей. В этом случае темп роста дохода = темпу роста трудовых ресурсов.

б) Т_р>S/b – в экономике увеличивается незанятость. В этом случае темп роста дохода определяется темпом роста К. Тогда фактический темп роста математически записывается так Т^У=min(Т_Р, Т_F), т.е. сбалансированный темп роста есть f темпов роста численности населения и капитала.

Ограниченность данных моделей задана предпосылками их анализа. Например, используемая в них производственная функция (Леонтьева) характеризуется отсутствием взаимозаменяемости факторов производства.

Модели Домара и Харрода неплохо описывали реальные процессы экономического роста 1920 – 1950гг., но для более поздних наблюдений (50-е – 70-е гг.) наиболее успешно использовалась неокласическая модель Р. Солоу.

Поиск по сайту: