Лінійна двійкова рекурентна послідовність у якості гами. Генератор псевдовипадкових чисел ANSI X9.17

При використанні асиметричних криптосистем виникає необхідність побудови надвеликих псевдовипадкових простих чисел.

Відповідні обчислювальні процедури включають алгоритми, що реалізовують етап тестування чисел на простоту.

У криптографічній практиці подібні алгоритми носять назву тестів. У основі тестів лежать т.з. критерії простоти.

Існує два типу критеріїв простоти: детерміновані і імовірнісні. Детерміновані тести дозволяють довести, що тестоване число – просте.

Практично застосовні детерміновані тести здатні дати відповідь не для кожного простого числа, оскільки використовують достатні умови простоти.

Детерміновані тести корисніші, коли необхідно побудувати велике просте число, а не перевірити простоту, скажімо, деякої єдиного числа.

На відміну від детермінованих, імовірнісні тести можна ефективно використовувати для тестування окремих чисел, проте їх результати, з деякою вірогідністю, можуть бути невірними. Проте, ціною кількості повторень тесту з модифікованими початковими даними, вірогідність помилки можна зробити як завгодно малою.

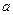Прикладом імовірнісного тесту є тест на основі малої теореми Ферма. Ця теорема стверджує, що якщо - просте, то для всіх , взаємно простих з , виконується умова (нерівність Ферма): 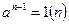. Таким чином, якщо умова теореми Ферма не виконана хоч би для одного числа в інтервалі , то - складове.

Тест на основі малої теореми Ферма полягає в наступному.

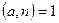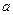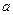Псевдовипадково обираємо лишок , перевіряємо умову . Якщо умова не виконана, означає, - складене. Перевіряємо нерівність Ферма (критерій простоти). Якщо воно не виконується, то число - складене. Інакше, повторюємо тест для іншого значення і так далі. Тест може давати невірні результати, оскільки існують складені числа , для яких, при деякому виконується умова малої теореми Ферма, наприклад .

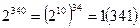Назвемо непарне складене число псевдопростим по підставі 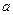, якщо пара задовольняє нерівність .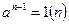

Можна показати, що якщо існує (взагалі кажучи, невідоме) основа 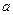, по якій не є псевдопростим, то при повторенні тесту Ферма вірогідність -кратного виконання нерівності 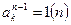рівна 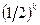. В цьому випадку вірогідність помилки тесту прямує до нуля із збільшенням .

Отже, вірогідність помилки може не знижуватися, лише якщо є псевдопростим для всіх (ненульових) підстав. Проте, такі числа існують. Вони називаються числами Кармайкла. Наприклад, числом Кармайкла є число .

Отже, тесту Ферма, взагалі кажучи, довіряти не можна. Проте цей тест є складовою частиною ряду інших тестів на простоту, оскільки його перевірочна умова є необхідною умовою простоти числа n.

Поиск по сайту: