АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Тест Соловея-Штрассена перевірки чисел на простоту

Читайте также:
  1. Алгебраическое представление двоичных чисел
  2. В чому полягає мета перевірки гіпотези про закон розподілу ряду?
  3. В10. Умение исполнить циклический алгоритм обработки массива чисел, записанный на алгоритмическом языке
  4. Виконання однократної перевірки доступності вузла (Ping), до якого має бути відправлено сигнал оповіщення
  5. Вопрос №2. Основные числовые множества. Некоторые свойства действительных чисел. Геометрическая интерпретация действ чисел. Окрестность точки.
  6. Для самоперевірки та підготовки до заліку (колоквіуму)
  7. Закон больших чисел
  8. Закон больших чисел. Неравенство Чебышева.
  9. Запропоновані види для перевірки та їх дані.
  10. Знаходження суми двох чисел.
  11. Использование зодиакальных атрибутов: цвета, чисел месяца, дней недели, металлов, камней
  12. Кодирование вещественных чисел

При тестуванні чисел на простоту за допомогою імовірнісного тесту, заснованого на малій теоремі Ферма, може виникнути ситуація, коли вірогідність помилки не знижується з кількістю повторень тесту.

В цьому випадку вона рівна одиниці і в результаті тестування може бути ухвалено невірне рішення. В зв'язку з цим розроблені і застосовуються на практиці імовірнісні тести, вільні від вказаного недоліку, наприклад, тест Соловея-Штрассена. При повторенні тесту Соловея-Штрассена разів, вірогідність неотбраковки| складеного числа . Істотно ефективнішим імовірнісним тестом є тест Рабіна-Міллера.

У тесті Рабіна-Міллера використовується критерій, заснований на факті, що для простого модуля квадратним коренем з одиниці є лише числа 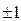, а для складеного непарного модуля , , число таких коренів більше двох.

Хай - непарне натуральне число. Тоді можна записати , де - непарне і . Якщо число - просте, то 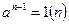, при . Тому квадратні корені з одиниці мають вигляд: 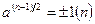, де показник рівний .

При витяганні квадратного кореня з одиниці по простому модулю ми або весь час одержуватимемо одиницю, або виникне корінь рівний .

Це означає, що у ряді лишків чисел 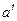, , по простому модулю або з'явиться , або всі вони дорівнюють одиниці, що можливо, коли .

Якщо - складене, то можливі і інші випадки.

Заснований на даному зауваженні тест Рабіна-Міллера полягає в наступному:

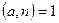1) псевдовипадково| обираємо лишок , перевіряємо умову . Якщо умова не виконана, означає, - складене і робота закінчена;

2) обчислюємо . Якщо , то не виключено, що число - просте і необхідно перейти на початок, щоб повторити тест для іншої підстави;

3) обчислюємо послідовно лишки чисел , по модулю , поки не з'явиться –1, або не вичерпається список;

4) якщо –1 виявлена в списку, то не виключено, що число - просте і необхідно перейти на початок, щоб повторити тест для іншої підстави;

5) якщо жодне число із списку не дорівнює –1, тео число - складене і необхідно закінчити роботу.

Назвемо складене число 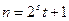, де , - непарний, сильно псевдопростим по основі , якщо виконується одна з двох умов: , або в послідовності , існує число, порівнянне з –1 по модулю .

Відомо, що такі складені числа, які при відповідних 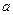проходять тест Рабіна-Міллера, існують.

Проте можна показати, що при повторенні тесту Рабіна-Міллера разів, вірогідність неотбраковки| складеного числа .

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.267 сек.)