Двочленні квадратичні порывняння. Властивості символу Якобі

Криптографічна система RSA є асиметричною криптосистемою, заснованою на односторонній функції з лазівкою, в якості якої вибрана степенева функція в кільці лишків цілих чисел по складеному (двупростому|) модулю . Стійкість системи зводиться до складності завдання факторизації великих двупростих| чисел.

Криптосистема RSA на кожному такті шифрування перетворить двійковий блок відкритого тексту довжини 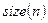, що розглядається як ціле число, за допомогою зведення в ступінь по модулю : 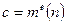. Показник ступеня і модуль є елементами відкритого (загальнодоступного) ключа. Лазівка забезпечується за рахунок секретного ключа, побудованого таким чином, що для всіх .

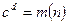Побудову криптосистеми забезпечує одержувач повідомлень. Спочатку випадковим чином вибираються два різні великі прості числа і . На практиці вибрані прості числа повинні задовольняти деяким додатковим умовам.

Потім обчислюється модуль , функція Ейлера від модуля 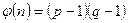, а також вибирається випадкове число 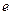, взаємно простої з .

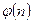Секретний ключ будується за допомогою розширеного алгоритму Эвкліда|, як число 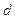, що задовольняє порівнянню 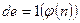. Потім всі дані, окрім 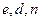, а також дані проміжних обчислень знищуються. Пара 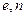оголошується в якості відкритого ключа.

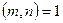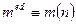Росшифрування| забезпечується двома фактами: для з теореми Ейлера виходить, що , крім того, для інших значень можна показати, що для модуля вигляду співвідношення також має місце. При побудові ключів можна використовувати функцію замість .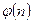

Цифровим підписом (ЦП|) називається результат спеціального криптографічного перетворення, здійсненого над електронним документом його власником. Мета перетворення – довести незаперечність тексту документа і факту перетворення даних конкретною особою. Основний метод – перевірка факту використання ключа (секретного параметра) підпису без знання самого ключа.

Підпис на основі RSA є блоком даних. Підписане повідомлення - це початкове повідомлення, передаване спільно з ЦП|.

Ідея ЦП|. Власник секретного ключа 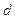криптосистеми RSA в якості підписаного повідомлення представляє пару . Дійсно, перетворення 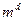може здійснити тільки він. Оскільки є в повідомленні в початковому вигляді, будь-який абонент в змозі перевірити співвідношення 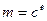, яке виконуватиметься лише у тому випадку, коли дійсно .

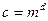Проте подібний підхід не забезпечує стійкість підпису при передачі випадкових даних. Дійсно, виберемо число 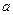і побудуємо повідомлення 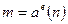. Тоді, очевидно, 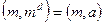, тобто підпис дійсний. З цієї причини замість 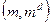слід використовувати пару 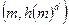, де 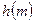- т.з. гэш-функція повідомлення , несекретне, наперед обумовлене перетворення. Перевірка підпису 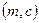починається з обчислення 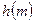, потім результат порівнюється з .

Поиск по сайту: