АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Тестування чисел на простоту. Імовірнісні та детерміновані тести. Тест на основі малої теореми Ферма

Читайте также:
  1. II етап-1993 р. - липень 1994 р. (етап початку масової малої та великої (акціонування) приватизації (роздержавлення), або законо-декрето-указовий період)
  2. Алгебраическое представление двоичных чисел
  3. В10. Умение исполнить циклический алгоритм обработки массива чисел, записанный на алгоритмическом языке
  4. Визначення потенційного ВВП на основі розриву ВВП. Вплив безробіття на динаміку ВВП.
  5. Визначення рівноважного ВВП на основі методу “видатки-випуск”.
  6. Висновки моделі IS-LM-BP для випадків малої та високої мобільності капіталів
  7. Вопрос №2. Основные числовые множества. Некоторые свойства действительных чисел. Геометрическая интерпретация действ чисел. Окрестность точки.
  8. Г) процеси переробки, виготовлення, тестування та складальні.
  9. Дані та припущення, на основі яких здійснено відстеження результативності.
  10. Детерміновані точка зору: Інтерполяція і наближені методи
  11. Домінантне заняття на основі музично – дидактичної гри «Музична абетка»
  12. Економічна рівновага на основі моделі AD-AS

 

При тестуванні чисел на простоту за допомогою імовірнісного тесту, заснованого на малій теоремі Ферма, може виникнути ситуація, коли вірогідність помилки не знижується з кількістю повторень тесту.

В цьому випадку вона рівна одиниці і в результаті тестування може бути прийнято невірне рішення. В зв'язку з цим розроблені і застосовуються на практиці імовірнісні тести, вільні від вказаного недоліку.

Імовірнісний тест Соловея-Штрассена використовує критерій Ейлера для визначення значення символу Лежандра: .

Основою тесту є наступне твердження.

 

Теорема. Непарне ціле число є простим тоді і тільки тоді, коли для всіх чисел 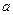: виконується нерівність вигляду .

Назвемо вказану нерівність співвідношенням Ейлера.

У цьому співвідношенні ліва частина обчислюється безпосередньо, а права частина – за правилами обчислення символу Якобі, який співпадає з символом Лежандра, якщо число n є простим.

Число n, що задовольняє співвідношенню Ейлера, називається Ейлеровим| псевдопростим з основою 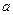. Відомо, що ейлерові| псевдопрості є псевдопростими числами.

З теореми випливає, що складених чисел, які були б ейлеровими| псевдопростими з будь-якою основою, не існує.

 

Тест Соловея-Штрассена аналогічний тесту Ферма.

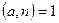Псевдовипадково обираємо лишок , перевіряємо умову . Якщо умова не виконана, означає, - складене. Перевіряємо співвідношення Ейлера. Якщо воно не виконується, то число - складене. Інакше, повторюємо тест для іншого значення .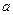

Якщо ми могли б перевірити співвідношення Ейлера для всіх , то ми змогли б точно визначити, чи є число простим. Але для великих це неможливо. Тому необхідно оцінити, як поводиться вірогідність помилки, при збільшенні числа повторень тесту.

Виявляється, при повторенні тесту Соловея-Штрассена разів, вірогідність неотбраковки| складеного числа .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)