Ключові системи потокових шифрів. Життєвий цикл ключів

Невироджена еліптична| крива над полем лишків за модулем пов'язана з рішеннями нерівність , .

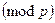Кожне рішення нерівності 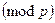називається крапкою. Безліч рішень нерівність 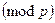можна розширити таким чином, що розширена множина стане комутативною групою 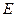. Ця група називається групою крапок на еліптичній кривій. Груповий закон в групі 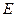називається складанням. Основною причиною, що дозволяє побудувати групу, є можливість побудови нових рішень рівняння кривої, виходячи з вже відомих. Виявляється, якщо дані рішення і то «практично завжди» можна знайти третє рішення, використовуючи знання координат перших двох. Операція, що зіставляє двом крапкам їх суму , в афіних| координатах записується у вигляді дробових виразів, тому при обчисленнях може виникнути особливість, якщо у відповідному знаменнику з'явиться нульове значення (по модулю ). Очевидно, це єдина ситуація, коли виникає особливість. Отже, їй можна зіставити деяке позначення () і розширити безліч рішень рівняння кривої, додавши символ О, імітуючи тим самим існування додаткового елементу, званого нескінченно видаленою крапкою. Якщо для операції «+» над крапками вважати нейтральним елементом, то розширена безліч точок кривої перетворюється на групу, а сама операція – в груповий закон. Нехай , 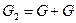і т.д. виходячи з крапки, можна побудувати послідовність точок довжини .

Якщо записувати подібне - кратне додавання на кривій у вигляді 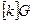, поклавши , то, очевидно, коефіцієнт можна приводити по модулю і розглядати вирази вигляду і 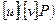. Операція 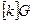називається скалярним множенням на . Найменше ціле , для якого , називається порядком крапки .

Груповий закон відповідає наступним правилам.

1. 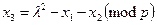, , 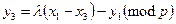де

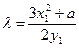
якщо і , якщо .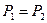

2. Якщо знаменник 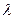перетворюється в нуль, то .

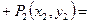
3. Операція, зворотна до складання:

4. Для будь-якої точки Р, .

Аналог протоколу Діффі-Хеллмана узгодження ключів. Хай задано рівняння невиродженої еліптичної кривої, а також точка великого простого порядку . Абонент А вибирає псевдовипадкове секретне число х, обчислює крапку і пересилає її абоненту В. Аналогічно, Абонент В вибирає псевдовипадкове секретне число у, обчислює крапку і пересилає її абоненту А. Далі абонент А обчислює , а абонент В обчислює , після чого абоненти будують загальний ключ, виходячи з крапки , відомої їм обом. 20. Груповий закон на невиродженій еліптичній кривій в афінних координатах. Аналог протоколу Діффі-Хеллмана а групі точок на еліптичній кривій.

Поиск по сайту: