Натуральный вывод в логике высказываний

Недостаток таблицы истинности – её абстрактность. В реальности же какие-то интуитивные ходы мысли подразумеваются у нас в уме. Элементарные правила выводимости:

Для конъюнкции:

· А, B ├ A & B (&⁺);

· A & B ├ A (&^-).

Для дизъюнкции:

· A v B, (V^-);

· A├ A v B (V⁺).

Импликация:

· A Ͻ B, A ├ B (Ͻ^-);

· A Ͻ B, B├ A (Ͻ^-)

Для отрицания:

1) Двойное отрицание – утверждение:

2) Правило отрицания для конъюнкции: ├

3) Правило отрицания для дизъюнкции: ├

4) Правило отрицания для импликации: ├

Данные правила позволяют обосновать практически все выводы, основываясь на входных данных. Однако если нет исходных данных, то мы допускаем допущения. Типичный пример – доказательство от противного. Допущение возможно тогда и только тогда, когда допущение будет исключено в ходе доказательства. Правила элементарных рассуждений – каким образом мы должны строить вывод, чтобы в дальнейшем избавиться от допущений. Есть 2 правила:

1. Правило допущения - если в процессе доказательства мы приняли какое-то допущение, то избавиться от допущения можно, если из какого-то А можно логически вывести В, то это означает, что между ними есть условная связь.

2. Правило от противного (доказательство от противного) – если мы допускаем неверность А и выводим какое-то В, а также из не А выводим не В, то неверно не не А, а само А. Если приходим к противоречию, то будет неверно само допущение, а не доказательство.

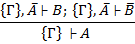
Например: «Если тело движется, то оно движется либо там, где оно есть, либо там, где его нет. Но тело не движется там, где оно есть, поскольку занимает равное себе место и не движется там, где его нет, т.к. без тела нет движения. Следовательно, движения не существует».

Формализуем данное высказывание (13):

«Тело движется» – А;

«Тело движется там, где оно есть» - В;

«Тело движется там, где его нет» - С.

Поиск по сайту: