Элементы логики предикатов

Есть необходимость анализа структуры простых высказываний. Это приводит к важной теории – логики предикатов. Например: «Водород легче углекислого газа». Это высказывание простое, т.е. «H₂ легче CO₂». Здесь присутствует именная группа H_2, которая обозначает некоторый конкретный предмет, состоящий из 2х атомов водорода. Такие именные группы называются имена (предметные константы) – категория собственных имен. Извлечем предметную константу. Останется «(…) легче CO₂». На незаполненное место можно подставить любой газ.

Такие ненасыщенные выражения называются предикатами. Предикат – это такое выражение, имеющее такое незаполненное место, при подстановке в которое можно получить ложное или истинное высказывание. Предикаты сопоставляют именам истину или ложь.

Такого рода предикаты называют одноместными предикатами («(…) легче CO₂»). Однако если CO₂ рассматривать как имя, тогда предикат будет иметь 2 незаполненных места («(…) легче (…)») -2хместный предикат. Также предикаты могут обладать многоместностью. Если заменить незаполненные имена любыми переменными и формализуем, то получим: Легче (х,у).

Предикаты – пропозициональные функции. Функция разъясняется через отображение между множествами. Множество – совокупность произвольных предметов, мыслимых как целое. Имеем множество из 3х элементов и другое множество из 3х элементов. Можно отобразить одно множество через другое через сопоставление элементов.

Биективное отображение – когда элементы одного множества взаимно сопоставлены элементам другого множества.

Также элементы множества могут сопоставляться элементам этого же множества и др.

Одно и то же отображение может строиться различными способами. Функция – способы построения отображений. Примеры функций: f(x)=y, x²=y, f(x,n)=y и т.д. Предикат – функция, которая отображает значение имен в область 2х абстрактных имен – 1-истина, 0 – ложь. Самый простейший варианты – когда рассматривается одноместный предикат. Например: Человек (х). Определим х на области живых существ. На месте одних будем получать – 1, других – 0. Например: Сократ – 1, кошка – 0.

Пропозиционарная функция отображает область определения на 1,0 D(f)à{1,0}. Однако кроме имен также можно использовать кванторы («Некоторые газы легче углекислого»), т.е. некоторые обобщенные выражения. В классической логики используются 2 квантора:

1) Квантор всеобщности (все, любой, каждый) – указывает на то, что переменная принимает значение любого предмета из предметной области. Обозначается, как

2) Квантор существования (некоторый, существует). Обозначается

Преобразуем предикаты, используя квантор (Некоторые газы легче углекислого):

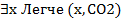
Кванторные выражения комбинируются с логическими союзами. Например: «Все люди смертны». Запишем: 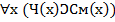. Пример: «Некоторые люди брюнеты». Это означает: .

Пример: «Все братья Маши женаты». Структура данного высказывания: брат – 2х местный предикат, т.е.

Пример: «Брат мужа Маши живет в Северске, а жена его в Новосибирске». Соответственно: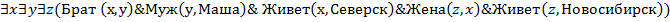

Первым шагом является задание неопределяемых терминов. Другими словами, их значение определяется из контекста.

Вторым шагом – все остальные термины вводятся по определению, отталкиваясь от терминов 2ой группы.

Третий шаг – формулируются высказывания.

Пример:

Мужчина (х)

Брак (х, у)

Ребенок (х, у)

Женщина (х) = (Def) ~ М (х) (не мужчина)

Брак и ребенок – это не свойства, а отношения между людьми.

1) Мать (х, у – икс игрику мать) = Женщина (х) & Ребенок (у,х)

2) Теща (х, у) = Женщина (х) & (Ребенок (z,x) & Женщина (z) & Брак (z,y)), т.е. теща – женщина, у которой существует ребенок женского пола (z), который состоит в браке с мужчиной (у).

3) Свекор (х,у) = Мужчина (х) & (Ребенок (z,x) & Мужчина (z) & Брак (z,y))

Формализуем данные высказывания:

Формальные многообразия – логические теории, где формальные высказывания содержат формальные математические записи.

Поиск по сайту: