 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Интерпретация высказывательных форм
Основные принципы для интерпретации высказывательных форм:
1. Любое высказывание обладает истинностным значением. Другими словами, если что-то является высказыванием, то оно должно быть или истинным или ложным. От этого мы не можем отречься.
2. Высказывание не может иметь более одного истинностного значения.
3. Истинностное значение сложных высказываний зависит от истинностных значений простых высказываний и от того, какие логические союзы их связывают. Если мы знаем значения А, В, С, то мы можем арифметически вычислить истинность всего высказывания.
Для вычисления истинности высказывания воспользуемся методом истинностных таблиц. Имеем высказывание А и мы знаем, что оно может быть истинным или ложным. Обозначим 1 – истина, 0 – ложь.
| А |
Отрицание меняет истинностное значение на противоположное.
| А | ~A |
Для бинарных логических союзов: для конъюнкции истина бывает тогда и только тогда, когда все высказывания будут истинными.
| A | & | B |
Дизъюнкция: истина тогда и только тогда, когда хотя бы одно высказывание является истинным.
| A | V | B |
Строгая дизъюнкция: совпадение значений означает ложь.
| A | 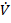
| B |
Импликация: когда из истины следует истина, это будет истинным; когда из лжи следует ложь, будет истина; когда из лжи следует истина, будет истина (Если сахар в воду не опускаем, то он может как раствориться, так и не раствориться). Если основание ложно, то следствие может быть каким угодно. Это говорит о том, что нельзя принимать ложные аргументы, т.к. отталкиваясь от них можно доказать любой тезис.
| A | Ͻ | B |
Эквиваленция (тождество): истинность, если значения одинаковы, ложность, если разные.
| A | ≡ | B |
Например: Иванов говорит, что Петров врет, Петров говорит, что Сидоров врет, а Сидоров говорит, что и Иванов, и Петров врут. Кто врет?
Для решения данной задачи необходимо построить алгоритм. Главная проблема – формализация. Представим это в виде:
Высказывание: «Иванов врет» будет истинно тогда и только тогда, если то, что он сказал, будет ложным и т.д.
Иванов врет – А; è A≡ 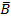
Петров врет – В; è B≡ 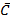
Сидоров врет – С. è C≡ 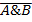
Далее необходимо проверить условие совместимости 3х высказываний, т.е. когда эти 3 утверждения будут истинными.
(A≡ 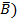 & (B≡
& (B≡ 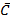 ) & (C≡
) & (C≡ 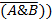
Итого имеем 8 возможностей. Количество истинностных возможностей определяется числом 2n, где n – число разных простых высказываний. Под буквой пишем возможные варианты для автоматизации процесса.
| (A | ≡ | 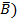
| & | (B | ≡ | 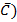
| & | (C | ≡ | 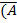
| 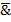
| 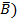
|
Ответ: Иванов врет, Сидоров врет, а Петров говорит правду.
Пример: в совершении преступления подозреваются 3 человека: Иванов, Петров, Сидоров. Они дали следующие показания: Иванов сказал: «Если преступление совершил Петров, то он ходил на дело вместе с Сидоровым», Петров сказал: «Преступление совершил Иванов или Сидоров», Сидоров сказал: «Я преступление не совершал». Кто совершил преступление, если:
1) Все говорят правду;
2) Все лгут;
3) Совершившие преступление лгут, несовершившие говорят правду;
4) Говорит правду только один;
5) Только один врет;
Решение:
Обозначим следующее:
Иванов совершил преступление – А;
Петров совершил преступление – В;
Сидоров совершил преступление – С.
Тогда:
1) Все говорят правду:
| (В | Ͻ | 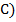
| & | (А | v | C) | & | (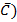
|
Ответ: Иванов совершил преступление.
2) Все лгут:
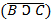
| & | 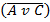
| & | (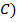
| ||||
3) Совершившие преступление лгут, несовершившие говорят правду;
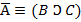
| & | 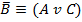
| & | |||||||||||||
Пример: Если имущество нажито в совместном браке, то оно делится в равных долях. Если имущество нажито не совместном браке, то оно делится в равных долях.
Поиск по сайту: