Методы экстраполяции

Вметодическом плане основным инструментом любого прогноза является схема экстраполяции. Сущность экстрапо­ляции заключается в изучении сложившихся в прошлом и нас­тоящем устойчивых тенденций развития объекта прогноза и переносе их на будущее.

Различают формальную и прогнозную экстраполяцию. Формальная базируется на предположении о сохранении в бу­дущем прошлых и настоящих тенденций развития объекта про­гноза; при прогнозной фактическое развитие увязывается с ги­потезами о динамике исследуемого процесса с учетом изменений влияния различных факторов в перспективе. Методы экстраполяции являются наиболее распространен­ными и проработанными. Основу экстраполяционных методов прогнозирования составляет изучение динамических рядов. Динамический ряд — это множество наблюдений, полученных последовательно во времени.

В экономическом прогнозировании широко применяется метод математической экстраполяции, в математическом смысле означающий распространение закона изменения фун­кции из области ее наблюдения на область, лежащую вне отрезка наблюдения. Тенденция, описанная некоторой функцией от времени, называется трендом. Тренд — это длительная тенден­ция изменения экономических показателей. Функция пред­ставляет собой простейшую математико-статистическую (трендовую) модель изучаемого явления.

Следует отметить, что методы экстраполяции необходимо применять на начальном этапе прогнозирования для выявле­ния тенденций изменения показателей. Рассмотрим методы экстраполяции.

Метод подбора функций — один из распространенных ме­тодов экстраполяции. Главным этапом экстраполяции тренда является выбор оптимального вида функции, описывающей эмпирический ряд. Для этого проводятся предварительная обработка и преобразование исходных данных с целью облег­чения выбора вида тренда путем сглаживания и выравнива­ния временного ряда. Задача выбора функции заключается в подборе по фактическим данным (x_i, y_i) формы зависимости (линии) так, чтобы отклонения (Δi) данных исходного ряда y_i от соответствующих расчетных y_i` находящихся на линии, бы­ли наименьшими (рис.). После этого можно продолжить эту линию и получить прогноз.

Расчет параметров (а, b) для конкретной функциональной зависимости осуществляется методом наименьших квадратов (МНК) и его модификаций. Суть МНК состоит в отыскании параметров модели тренда, минимизирующих отклонения рас­четных значений от соответствующих значений исходного ря­да, т.е. искомые параметры должны удовлетворять условию где п — число наблюдений.

Выбор модели осуществляется с помощью специально раз­работанных программ. Есть программы, предусматривающие возможность моделирования экономических рядов по 16-ти функциям: линейной, гиперболической различных типов, экспоненциальной, степенной, логарифми­ческой и др. Каждая из них может иметь свою, специфическую область применения при прогнозировании экономических яв­лений.

Так, линейная функция (у = а + bх) (рис.) применяется для описания процессов, равномерно развивающихся во време­ни. Параметр b (коэффициент регрессии) показывает скорость изменения прогнозируемого у при изменении х.

Гиперболы (рис.) хорошо описывают процессы, характе­ризующиеся насыщением, когда существует фактор, сдержива­ющий рост прогнозируемого показателя.

Модель выбирается, во-первых, визуально, на основе сопос­тавления вида кривой, ее специфических свойств и качествен­ной характеристики тенденции экономического явления; во-вторых, исходя из значения критерия. В качестве критерия чаще всего используется сумма квадратов отклонений 5. Из со­вокупности функций выбирается та, которой соответствует ми­нимальное значение 5.

Прогноз предполагает продление тенденции прошлого, вы­ражаемой выбранной функцией, в будущее, т.е. экстраполяцию динамического ряда. Программным путем на ЭВМ определяет­ся значение прогнозируемого показателя. Для этого в формулу, описывающую процесс, подставляется величина периода, на который необходимо получить прогноз. В связи с тем, что этот метод исходит из инерционности экономических явлений и предпосылок, что общие условия, определяющие развитие в прошлом, не претерпят существен­ных изменений в будущем, его целесообразно использовать при разработке краткосрочных прогнозов обязательно в соче­тании с методами экспертных оценок. Причем динамический ряд может строиться на основании данных не по годам, а по месяцам, кварталам.

Экстраполяция методом подбора функций учитывает все данные исходного ряда с одинаковым "весом". Классический метод наименьших квадратов предполагает равноценность исходной информации в модели. Однако, как показывает опыт, экономические показатели имеют тенденцию "старе­ния". Влияние более поздних наблюдений на развитие про­цесса в будущем существеннее, чем более ранних. Проблему "старения" данных динамических рядов решает метод экспоненциалъного сглаживания с регулируемым трендом. Он поз­воляет построить такое описание процесса (динамического ряда), при котором более поздним наблюдениям придаются большие "веса" по сравнению с более ранними, причем "веса" наблюдений убывают по экспоненте. В результате создается возможность получить оценку параметров тренда, характери­зующих не средний уровень процесса, а тенденцию, сложив­шуюся к моменту последнего наблюдения.

Скорость старения данных характеризует параметр сглажи­вания а. Он изменяется в пределах 0 < а < 1.

В зависимости от величины параметра прогнозные оценки по-разному учитывают влияние исходного ряда наблюдений: чем больше а, тем больше вклад последних наблюдений в формирование тренда, а влияние начальных условий быстро убы­вает. При малом а прогнозные оценки учитывают все наблюдения, при этом уменьшение влияния более "старой" информации происходит медленно, т.е. чем меньше а, тем дан­ные более стабильны, и наоборот.

В области экономического прогнозирования наиболее употребимы пределы 0,05 < а < 0,3. Значение а в общем случае должно зависеть от срока прогнозирования: чем меньше срок, тем большим должно быть значение параметра.

Этот метод реализуется на ЭВМ с помощью специально раз­работанных программ в блоке "временные ряды", который яв­ляется составной частью пакета экономических расчетов.

4. Методы моделирования и экономико-математические методы.

Моделирование предполагает конструирование модели на основе предварительного изучения объекта или процесса, выделения его существенных характеристик или признаков. Прогнозирование экономических и социальных процессов с использованием моделей включает разработку модели, ее эк­спериментальный анализ, сопоставление результатов про­гнозных расчетов на основе модели с фактическими данными состояния объекта или процесса, корректировку и уточнение модели.

В зависимости от уровня управления экономическими и со­циальными процессами различают макроэкономические, ме­жотраслевые, межрайонные, отраслевые, региональные модели и модели микроуровня (модели развития фирмы).

По аспектам развития экономики выделяют модели прогно­зирования воспроизводства основных фондов, трудовых ре­сурсов, цен и др. Существует ряд других признаков классифи­кации моделей: временной, факторный, транспортный, производственный.

Рассмотрим некоторые из наиболее разработанных эконо­мико-математических моделей, получивших широкое приме­нение в практике прогнозирования экономики за рубежом (особенно в США) и используемых (эпизодически) в странах СНГ.

К матричным моделям относятся модели межотраслевого баланса (МОБ): статические и динамические. Первые предназ­начены для проведения прогнозных макроэкономических рас­четов на краткосрочный период (год, квартал, месяц), вторые — для расчетов развития экономики страны на перспективу. Они отражают процесс воспроизводства в динамике и обеспечивают увязку прогноза производства продукции (услуг) с инвестици­ями.

Статическая модель МОБ в системе баланса народного хо­зяйства имеет вид

где a_ij — коэффициенты прямых затрат; x_j — объем производства продукции j-ой отрасли-потреби­теля (j = 1.n); X_i — валовое производство продукции (услуг) i-ой отрасли-производителя (i=l,n); Yi — объем конечного продукта i-й отрасли-производителя.

Выражение 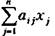характеризует межотраслевые потоки и в целом промежуточный продукт; - конечный продукт; 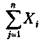— валовой общественный продукт.

Упрощенная динамическая модель включает индекс года.

При переходе к Системе национальных счетов (СНС) моде­ли межотраслевого баланса претерпевают некоторые изменения. Выражение характеризует промежуточное потребление в сферах материального производства и нематериальных услуг; Y — конечное использование валового нацио­нального продукта (ВНП) по i-й отрасли, включающее конеч­ное потребление (потребление домашних хозяйств и государственные расходы), валовое накопление и экспорт; х_j — валовой выпуск i-й отрасли.

Сформированный на основе моделей межотраслевой ба­ланс может использоваться для решения многих задач: про­гнозирования макроэкономических показателей, межотрас­левых связей и потоков (поставок), структуры экономики, отраслевых издержек, динамики цен, показателей эффектив­ности производства (материало-, энерго-, металло-, химико-и фондоемкости).

Модели оптимального планирования используются для оп­ределения оптимального варианта функционирования эконо­мики в целом и ее отдельных звеньев. Экономико-математи­ческая модель представляет собой формализованное описание экономического процесса и состоит из целевой функции и сис­темы ограничений. Целевая функция описывает цель оптимиза­ции и представляет собой зависимость показателя, по которому ведется оптимизация, от независимых переменных. Влияние каждой из переменных на величину целевой функции выража­ется коэффициентом — значением показателя, экстремум кото­рого используется в качестве критерия оптимальности. Систе­ма ограничений отражает объективные экономические связи и зависимости и представляет собой систему равенств и нера­венств. На макроуровне критерием оптимальности является максимум валового национального продукта. На микроуровне в качестве критерия оптимальности могут быть использованы экстремумы показателей: максимум прибыли, минимум затрат, максимум выпуска продукции (услуг) и др.

Модели по расчету оптимального варианта производства продукции имеют следующий общий вид: целевая функция: f(x) -> max (min) и система ограничений

На макроуровне расчеты производятся в агрегированном ви­де. Система ограничений претерпевает некоторые изменения. В частности, вместо ограничения по фонду времени работы обору­дования вводятся ограничения по фондоемкости или производ­ственной мощности (на отраслевом уровне), развернутый ассор­тимент (конкретные виды продукции) заменяется групповым.

Следует отметить, что, несмотря на многообразие разрабо­танных моделей и наличие пакетов программ для проведения много вариантных расчетов, оптимизационные задачи в респуб­лике носят, как правило, экспериментальный характер. Глав­ными причинами, сдерживающими их внедрение в практику прогнозных и плановых расчетов как на макро-, так и на микро­уровне, являются: а) неадекватность разрабатываемых моделей реальным экономическим процессам; б) отсутствие специалис­тов-практиков, хорошо владеющих моделированием экономи­ческих и социальных процессов и методами оптимизации; г) проблема информационного обеспечения.

Экономико-статистические модели используются для ус­тановления количественной характеристики связи, зависи­мости и взаимообусловленности экономических показателей. Система такого рода моделей включает: одно-, многофактор­ные и эконометрические модели. Примеры однофакторных мо­делей:

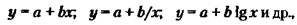
где у — значение прогнозируемого показателя; а — свободный член, определяющий положение начальной точки линии рег­рессии в системе координат; х — значение фактора; b — пара­метр характеризующий норму изменения у на единицу х.

Многофакторные модели позволяют одновременно учиты­вать воздействие нескольких факторов на уровень прогнозиру­емого показателя. При этом последний выступает как функция от факторов:

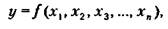гдех,, х₂, х₃,..., х„ — факторы.

При линейной зависимости многофакторные модели могут быть представлены следующим уравнением:

где а₀ — свободный член; а₁ а₂ а_п — коэффициенты регрессии, показывающие степень влияния соответствующего фактора на прогнозируемый показатель при фиксированном значении ос­тальных факторов.

При нелинейной зависимости многофакторная модель мо­жет иметь вид

Многофакторные модели используются при прогнозирова­нии макроэкономических показателей, показателей спроса на продукцию, себестоимости, цен, прибыли и др.

Эконометрической моделью называют систему регресси­онных уравнений и тождеств, описывающих взаимосвязи и зависимости основных показателей развития экономики. Система экономико-математических моделей эконометрического типа служит для описания сложных социально-эко­номических процессов. Факторы (переменные) эконометри­ческой модели подразделяются на экзогенные (внешние) и эндогенные (внутренние). Экзогенные переменные выбира­ются так, чтобы они оказывали влияние на моделируемую систему, а сами ее влиянию не подвергались. Они могут вво­диться в модель на основе экспертных оценок. Эндогенные пе­ременные определяются путем решения стохастических и тождественных уравнений. Для каждой эндогенной перемен­ной методом наименьших квадратов оценивается несколько вариантов регрессионных уравнений и выбирается лучший для включения в модель. Например, инвестиции производ­ственного назначения зависят от суммы прибыли (эндоген­ный фактор) и индекса цен на инвестиционные товары (экзо­генный фактор). Органичной частью эконометрической модели может быть и межотраслевой баланс. Обычно коли­чество уравнений модели равно количеству эндогенных пере­менных.

Эконометрические модели позволяют прогнозировать ши­рокий круг показателей (ВНП, доходы населения, потребление товаров и услуг и др.) В условиях автоматизации расчетов соз­дается возможность разработки альтернативных вариантов развития экономики с учетом изменений внешних и внутрен­них условий (факторов). Следует отметить, что использование эконометрических моделей требует создания банков данных и подготовки высококвалифицированных специалистов по раз­работке и реализации этих моделей.

Цель имитационного моделирования состоит в воспроизве­дении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между ее эле­ментами. Имитационные модели позволяют воспроизводить реальные процессы и предвидеть результаты различных дей­ствий. Например, имитационную модель оптимизационного процесса можно представить как систематическое изменение значений управляемых переменных с последующим получени­ем результатов прогноза и их анализа.

Модели принятия решений основываются на теории игр и применяются в условиях неопределенности или в ситуациях, когда интересы сторон не совпадают. Каждая из сторон прини­мает такие решения, т.е. выбирает такую стратегию действий, которая с их точки зрения обеспечивает наибольший выигрыш или наименьший проигрыш. Причем каждой из сторон ясно, что результат зависит не только от собственных действий, но и от действий партнеров. Например, противоборство конкурен­тов в процессе борьбы за рынок сбыта конкретного вида про­дукции.

Модели сетевого планирования применяются с целью сокра­щения сроков выполнения сложных проектов и других работ и оптимального использования предназначенных для этого ре­сурсов.

Термин "сетевое планирование" приобретает в последнее время большую популярность. Основой сетевого планирова­ния служит изображение комплекса взаимосвязанных работ в виде графа, обычно именуемого сетевым графиком, стрелочной диаграммой, логической сетью или сетевой моделью. В сетевом графике отражается последовательность этапов планирования, необходимых для достижения заранее поставленной цели.

Примером сетевых методов планирования является метод ПЕРТ-время, или ПЕРТ-затраты.

Экономико-математические модели могут быть реализова­ны с помощью экономико-математических методов (ЭММ). ЭММ представляют собой способы (приемы) расчета экономи­ческих показателей с применением методов прикладной мате­матики и математической статистики. С помощью ЭММ появляется возможность всестороннего обоснования измене­ния экономических показателей. Они позволяют повышать ка­чество прогнозов, осуществлять многовариантные оптимиза­ционные расчеты. Среди важнейших экономико-математических методов, ис­пользуемых в прогнозировании и планировании экономичес­ких и социальных процессов как в нашей стране, так и за рубе­жом, следует выделить: метод межотраслевого баланса, методы оптимизации (симплекс-метод и др.), корреляционно-регрес­сионный метод.

Метод межотраслевого баланса базируется на принципах разработки межотраслевого баланса, которые были обоснова­ны специалистами бывшего СССР и развиты за рубежом (В. Леонтьевым в США). Использование метода на основе моде­ли межотраслевого баланса позволяет осуществлять прогно­зирование развития экономики и ее отраслевой структуры исходя из конечных потребностей (конечного использования ВНП).

Процесс разработки межотраслевого баланса подразделя­ется на ряд последовательных этапов: 1) определение объема и отраслевой структуры конечного продукта (конечного использования ВНП) в прогнозируемом периоде; 2) раз­работка коэффициентов прямых материальных затрат по каждой отрасли на прогнозируемый период; 3) расчет коэф­фициентов полных затрат на производство единицы конечно­го продукта (конечного использования ВНП); 4) определение прогнозируемых объемов производства продукции по каждой отрасли исходя из коэффициентов полных затрат и намечаемых объемов конечного продукта (конечного ис­пользования ВНП); 5) формирование структуры выпуска продукции с выделением промежуточного потребления и конечного использования по каждой отрасли. В математи­ческой форме межотраслевой баланс представляет собой систему уравнений преобразований формируется матрица коэффициентов пол­ных затрат. Расчет производится на ЭВМ с помощью специ­альной программы обращения матрицы. Путем умножения матрицы коэффициентов полных затрат на матрицу (вектор) У конечного продукта (конечного использования ВНП) рас­считывается объем производства продукции (услуг) по каж­дой отрасли.

Затем на основе представленной выше системы уравнений производится расчет межотраслевых поставок, в целом проме­жуточного продукта и формируется таблица межотраслевого баланса, адекватная модели МОБ.

В настоящее время проводятся исследования по совершен­ствованию методики разработки прогнозного межотраслевого баланса в системе национальных счетов.

К методам оптимизации относятся линейное (сим­плекс-метод) и целочисленное программирование. С помощью методов оптимизации создается возможность выбора опти­мального варианта использования ресурсов и удовлетворения потребностей в продукции, размещения производительных сил, рационального прикрепления поставщиков к потребите­лям и решения других задач.

Оптимизационные расчеты осуществляются на основе разработанных экономико-математических моделей и исход­ной информации с использованием специальных пакетов программ и ЭВМ. Программно формируется матрица, в кото­рой отражаются коэффициенты затрат, тип и вектор ограни­чений, а также коэффициенты целевой функции. С помощью методов оптимизации производится расчет, в процессе кото­рого осуществляется выбор оптимального варианта в соот­ветствии с целевой функцией в рамках установленных огра­ничений.

Результаты оптимизационных расчетов носят рекоменда­тельный характер. Можно проводить множество расчетов, из­меняя ограничения по ресурсам, спросу на продукцию в связи с изменяющимися условиями. Желаемых результатов можно достичь путем работы с ПЭВМ в диалоговом режиме.

Сущность корреляционно-регрессионного метода заклю­чается в определении зависимости показателя от различных факторов. Этот метод предполагает установление наличия корреляционной связи между прогнозируемым показателем и влияющими на него факторами, определение формы связи, составление уравнения и осуществление прогноза на его ос­нове. Форма связи характеризует изменение значений одного признака в зависимости от изменения другого. Она может быть линейной и нелинейной и выражаться уравнениями. Одновременно с установлением фор­мы связи определяется теснота связи, которую характеризует коэффициент корреляции R.

Поиск по сайту: