Решение по Нейману - Моргенштерну

Дележи, входящие в С-ядро, не доминируются другими дележами, но сами доминировать другие не могут, поэтому выбор дележа из С-ядра - решение трудно оспоримое, но далеко не самое лучшее.

Разумеется, идеальным было бы указание такого дележа, который не только не доминировался какими-либо другими дележами, но и сам бы доминировал любой другой дележ. Приемлемые результаты можно получить путем некоторого расширения класса дележей подобно введению смешанных стратегий для решения антагонистических игр.

Такое расширение было произведено Дж. фон Нейманом и О. Моргенштерном путем использования понятий внутренней и внешней устойчивости.

Под внутренней устойчивостью множества дележей, образующих решение, понимается не доминирование дележей внутри решения. Под внешней устойчивостью понимается свойство доминирования хотя-бы одним из дележей, входящих в решение, любого дележа не входящего в решение.

Решением по Нейману-Моргенштерну (Н-М решением) кооперативной игры называется такое множество R дележей, что:

1. Никакие два дележа из R не доминируют друг друга (внутренняя устойчивость);

2. Каким бы ни был дележ S R найдется дележ r R такой, что r dom s (внешняя устойчивость).

Теорема связи между С-ядром и Н-М решением: Если в кооперативной игре существует С-ядро и Н-М решение R, то С Ì R.

Теорема. Если некоторое Н-М решение кооперативной игры <I,v> состоит из единственного дележа х, то характеристическая функция v является несущественной. (Н-М решение существенной кооперативной игры не может состоять только из одного дележа).

Недостатки Н-М решения:

1. Известны примеры кооперативных игр, которые не имеют Н-М решения. Более того, в настоящее время не известны какие-либо критерии, позволяющие судить о наличии у игры Н-М решения. Тем самым заложенный в Н-М решении принцип оптимальности не является универсально реализуемым и область его реализуемости пока остается неопределенной.

2. Кооперативные игры, если имеют Н-М решение, то, как правило, более одного. Поэтому принцип оптимальности, приводящий к Н-М решению не является полным: он не в состоянии указать игрокам единственной системы норм распределения выигрыша.

3. Решения существенных кооперативных игр состоят из более чем из одного дележа. Таким образом, даже выбор какого-либо конкретного Н-М решения еще не определяет выигрыша каждого из игроков.

Эти недостатки не "пороки", которые следовало бы исправлять, а недостатки, которые хотелось бы восполнить. Это отражает положение дел в действительности: большинство экономических и социальных проблем допускает множественные решения, и эти решения не всегда поддаются непосредственному сравнению по их предпочтительности.

Вектор Шепли.

До сих пор были рассмотрены решения игр, отвечающие принципам оптимальности в смысле выгодности и устойчивости (maxmin в чистых или смешанных стратегиях) или только устойчивости (C-ядро и Н-М решение в кооперативных играх). Рассмотрим решения, оптимальные в смысле справедливости.

Задача состоит в том, чтобы найти вектор распределения общего выигрыша между участниками игры: Ф(v) = (Ф₁(v), Ф₂(v),... Ф_n(v))

При этом необходимо, чтобы Ф(v) был дележом в условиях кооперативной игры, то есть отвечал бы требованиям индивидуальной и групповой рациональности.

Предлагаемое решение носит аксиоматический характер, то есть выводится формальным образом из некоторой полной и непротиворечивой системы аксиом. Эта система включает в себя: аксиому эффективности, аксиому симметрии и аксиому агрегации.

Аксиома эффективности: распределение выигрыша носителя игры (N) происходит только между игроками, входящими в носитель. Иными словами, все приращение выигрыша, достигаемое только за счет обьединения в коалицию (эффект супераддитивности), распределяется только между теми, кто его обеспечил. С другой стороны, все болваны получают только то, что они выиграли бы в одиночку или в составе коалиции.

Формально эти условия выражаются в том, что å Ф_i(v) = v (N), iÎN, и Ф_j(v) = v(j), jÎ I\N.

Аксиома симметрии: игроки, входящие в игру симметрично, должны получать одинаковый доход. Здесь симметричность понимается как одинаковое влияние на характеристическую функцию. Это утверждение равносильно тому, что доход игрока не зависит от его номера или "имени".

Формально Ф_j(v) = Ф_pj(v), где p - целое положительное число.

Аксиома агрегации: если игрок принимает участие в двух играх с характеристическими функциями v’ и v”, то причитающаяся ему доля:

Ф(v’ + v”) = Ф(v’) + Ф(v”), если множества игроков в обоих играх совпадают.

Совокупность аксиом является непротиворечивой и полной: для всякой характеристической функции v вектор Ф(v) существует и является единственным (вектор Шепли). Непротиворечивость обеспечивает существование, а полнота его единственность.

Теорема. Для любой характеристической функции v над I={1,2,...n} компоненты вектора Шепли определяются по формуле

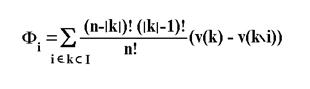
Пример. Для кооперативной игры трех лиц в 0-1 редуцированной форме эта формула имеет вид: Ф_i(v) = 1/6 (2 - 2C_i + C_j + C_f).

Следовательно, координаты вектора Шепли:

Ф₁(v) = 1/6 (2 - 2C₁ + C₂ + C₃), где C₁ = v(2,3);

Ф₂(v) = 1/6 (2 - 2C₂ + C₁ + C₃), где C₂ = v(1,3);

Ф₃(v) = 1/6 (2 - 2C₃ + C₁ + C₂), где C₃ = v(1,2).

Для того, чтобы вектор Шепли принадлежал к С-ядру необходимо и достаточно, чтобы выполнялось неравенство: 4C_i + C_j + C_f £ 4 для всех i, j, f.

Поиск по сайту: