АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема Гаусса. Поле бесконечно протяженной заряженной плоскости и двух заряженных параллельных плоскостей

Читайте также:
  1. S-M-N-теорема, приклади її використання
  2. V2: ДЕ 29 - Введение в анализ. Предел функции на бесконечности
  3. А — одностороннее боковое освещение; б — двустороннее боковое освещение; в — верхнее освещение; г — комбинированное освещение: 1 — уровень рабочей плоскости
  4. Бесконечно - малые последовательности
  5. Бесконечно большие и бесконечно малые функции
  6. БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ
  7. Бесконечно большие функции и их связь с бесконечно малыми функциями.
  8. Бесконечно малые и бесконечно большие функции
  9. Бесконечно малые функции
  10. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА
  11. Бесконечнозначная логика как обобщение многозначной системы Поста
  12. В БЕСКОНЕЧНО УДАЛЕННОЙ ТОЧКЕ

 

Теорема Гаусса: поток вектора напряженности электрического поля через любую замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на e0

 

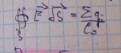
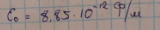
Поле бесконечно протяженной заряженной плоскости

Вывод формулы 1 вариант:{

Пусть σ — поверхностная плотность заряда на плоскости (рис. 4). Так как образующие цилиндра параллельны линиям напряженности (α = 90°, cos α = 0), то поток через боковую поверхность цилиндра отсутствует, и полный поток через поверхность цилиндра равен сумме потоков через два основания. Внутри цилиндра заключен заряд q = σS, поэтому, согласно теореме Остроградского-Гаусса, 2ES=σSε0ε}

 

По конспекту:

s=Q/S, σ − поверхностную плотность заряда

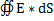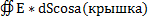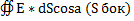= + + =ES0 + ES0 +0=2ES0 = sS0/e0


E=s/2e0

 

Поле двух заряженных параллельных плоскостей.

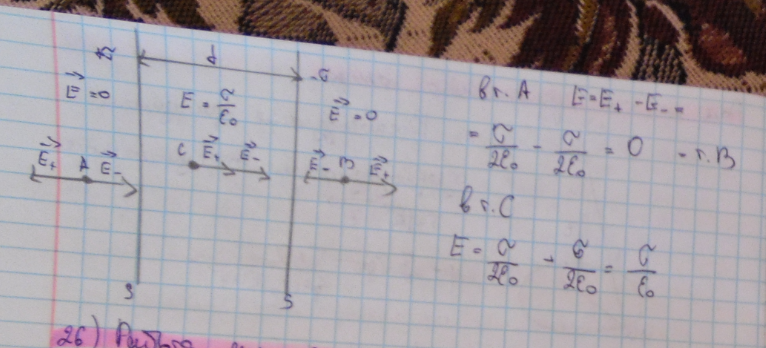
Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля E = 0.

В области между плоскостями E+ + E− (E+ и E− определяются по формуле ), поэтому результирующая напряженность: .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

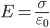Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)