АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Математические модели монтажного пространства

Читайте также:
  1. Can-Am-2015: новые модели квадроциклов Outlander L и возвращение Outlander 800R Xmr
  2. V. Идеология и практика модели «общенародного государства»
  3. V2: ДЕ 11 - Векторные пространства. Линейные операции над векторами
  4. V2: ДЕ 14 – Векторные пространства. Коллинеарность векторов.
  5. YIII.5.2.Аналогия и моделирование
  6. Авторегрессионные модели временных рядов
  7. Алгоритм моделирования по принципу Dt.
  8. Алгоритм моделирования по принципу особых состояний.
  9. Алгоритмизация модели и её машинная реализация
  10. Анализ деятельности Финской спортивной федерации по модели процесса эффективности функционирования
  11. Анализ эффективности использования ОС: факторные модели фондорентабельности и фондоотдачи
  12. Аналитические модели

 

Под монтажным пространством типовой конструкции понимается метрическое пространство, в котором устанавливается вход в неё типовых конструкций предыдущих уровней, и выполняются элементные соединения их выводов.

Метрические параметры – габарит размеры зоны монтажа, допустимая ширина проводников и зазоров между ними, координаты и размеры внешних монтажных площадок, размеры модулей, координаты и размеры их контактов. К математическим моделям монтажного пространства применяют высокие требования по степени формализации требования, соответствия при отображении метрических параметров и топологических свойств конструкции.

Топологические свойства – число слоев многослойной печатной платы (МПП), число переходов со слоя на слой, наличие замкнутых областей, запрещение для проведения соединений, ограничение на количество проводников, провод к 1 выводу.

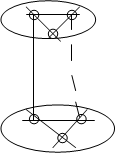
Монтажное пространство чаще всего имеет прямоугольную форму. Для тип конструкции, начиная с субблока и выше, характерно регулярное монтажное пространство. В качестве математической модели монтажного пространства используют неориентированный топологический граф Gr. Плоскость монтажного пространства разбивается на элементарные площадки, строка которой равна шагу положения проводников по соответствующем направлении. Чаще всего это квадраты. Далее каждый элемент площадки ставят в соответствие вершинам графа решетки. Две вершины соединяют ребром, если между соответствующими элементами площадками можно провести соединение с учетом метрических и топологических параметров тип конструкции установленной в данном монтажном пространстве.

Фрагмент печатной платы:

 
 

 

 


Граф решетки

 

 
 

 

 


Если можно проводники проводить под углом 45, то каждой вершине будет инцидентно 8 ребер.

Принцип реализован соединением в МПП.

 

n

 

 

n+1

 

Если соединение выполнено в любом направлении, то вершины графа сопоставляются выводам конструкции элемента.

 

 
 

 

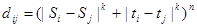dij – расстояние между j и j узлом решетки, где m – число узлов решетки.

S, t –координаты по осям у и х.

(*)
При ортогональной трассировки n=k=1

 

 
 

 

 

Предположим, что в сетке координат расположено монтажное пространство

 

 
 


G

 

 

Неориентированный граф

 

Расчет суммарной длины соединений между модулями:

1. Строят матрицы расстояний Dr, элементы которого рассчитаны по (*)

Пусть s=t=1

 

 

           
=Dr
1

          
           
           
           

 

 

2. Строится матрица геометрии Dg как по элементное * матрица Dr и матрица смежности R.

 

 

R=

           
           

 

Dg=

           
           
           
           

 

3. Суммарная длина ребер графа определяется как полу сумма элементов матрицы Dg.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)