 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Итерационный алгоритм компоновки
|
Читайте также: |
Предназначен для улучшения некоторой исходной компоновки методом парной или групповой перестановки элементов из одной части схемы в другую т. о., чтобы оптимизировать целевую функцию с учетом заранее ограничена. Начальную компоновку можно получить вручную или последовательным алгоритмом.
Идея парных перестановок.
Положим, что лучший вариант компоновки соответствует минимум некоторого показателя F. Пусть множество элементов Е разбито на два узла А и В и обозначим исходный вариант компоновки через К0, а значение целевой функции через F0. Предположим, что выбрана пара элементов аiÎА и biÎВ таких, что перестановка их местами приводит к уменьшению целевой функции. После их перестановки получаем К1 и F1, причем DF1=F1 – F0 > 0. Процесс перестановок повторяется до тех пор пока существует перестановка, которая < F. В результате получим серию вариантов K0, K1…Ki и Ki, которым соответствуют F0,F1…Fi и Ki, причем значение перестановок таково, что мы получаем монотонно убывающую последовательность F.
Такой итерационный процесс может привести к локальному минимуму.
Пройти локальный оптимум позволяет метод групповых перестановок. Обмен идет группами элементов, а не парами.
Рассмотрим один из способов выделения группы. Для всех пар аiÎА и biÎВ DF выбираем пару элементов А1 и В1 с макс DF временно осуществляем их перестановку. Процесс повторяем К раз до тех пор пока все элементы подмножества А и В не поменяются местами. Далее строится зависимость DF от шага обмена К.
По полученной кривой определяют шаг обмена К*, при котором значение p>0 максимально для
 |
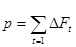некоторого ряда при t=1,…,k
Выполняем обмен группами a1,a2….ak из узла А в группы b1,b2….bк из узла В.
Произведение группового обмена улучшает его критерий между элементами связей.
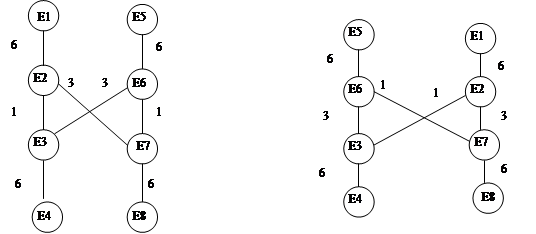Рис исходной компоновки Результат обмена
А В А В
В этом рисунке, если делать обмен одной парой элементов, то не уменьшает число меж соединений. Переносим элементы Е5 и Е6 из В в А и наоборот приводит к уменьшению меж узловых связей с 6-го до 2-го.
Итерационные алгоритмы дают лучшее качество решения, чем последовательные, но повышают затраты машинного времени. Для окончания итерации процессу задают число итераций или задают требуемую точность в виде условия:
Поиск по сайту: