Постановка задачи размещения. Критерии оптимизации

Т. к. очень много факторов влияет на решение задачи, то она разбивается на два этапа: размещение и трассировка. Сначала размещение, потом трассировка. Исходные данные:

1. Схема соединения элементов.

2. Метрические параметры и топологические свойства монтажного пространства.

Имеем множество элементов и множество цепей. Монтажное пространство определяется множеством фиксированных позиций. Необходимо найти такое отображение множества элементов во множество позиций, при котором достигается максимум целевой функции.

Критерий оптимизации:

1. Минимальная суммарная длина всех соединений или длина самой длинной связи.

2. Минимальное число пересеченных связей.

3. Максимизация числа цепей с простой конфигурацией.

4. Максимально близкое расположение модулей, имеющих наибольшее количество связей между собой.

Для n элементов и m позиций существует множество А = {ai/l=1,L} возможных размещений.

L=M!/(M-N)! при M>N.

L=M! при M=N.

Рассмотрим задачу размещения, как задачу квадратичного назначения. Математическая модель – взвешенный неориентированный граф, вершины – элементы схемы, полные подграфы – цепи. Связанность – матричные соединения.

, где |Qij| - число цепей, в которых входные элементы Еi и Ej.

Pq=1/(pq-1) – вес q-й связи

pq – количество элементов, соединенных q-й связью.

Математическая модель монтажного пространства – это граф решеткиGr.

Расстояние между позициями установки определяется матрицей расстояний этого графа Dr как правило, внешним выводам сопоставляется элемент e_0. Соединения с внешним выводом учтем вектором – столбцом взаимных связей H={hi/i=1,N}. Внешние выводы обычно фиксированы на периферии входных конструкций.

S 1 2 3 4 5

A

B

C

D

E

t(m)

Обозначим mi номер вероятностного ряда, где располагаются элементы ei. Тогда для некоторого размещения суммарная взвешенная длина соединения La будет вычисляться

(*)

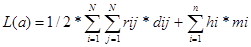dij- элемент матрицы Dr, определяет расстояние между ei и ej

I – слагаемое – полу сумма элементов матрицы геометрии D

В итоге требуется найти L(a) на множестве размещений А.

Математическим методом решения данной задачи является метод ветвей и границ.

Поиск по сайту: