 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Постановка задачи компоновки. Критерии оптимизации и ограничения
Задача компоновки заключается в определении схемного состава типовой конструкции каждый уровня. Эта задача решается обычно снизу вверх, т. е. известна схема соединения элементов i-1 -го уровня, необходимо распределить их по типовым конструкциям i-го уровня. Можно выделить 2 метода решения этой задачи:
- разрезание – разрезание схемы соединения элементов i-1 уровня на части заданного размера. Эта задача характерна для типовых конструкций, начиная с уровня субблока.
- покрытие – переход от схемы электрической функциональной к схеме электрической принципиальной.
Задача покрытия сложнее, чем разрезания, т. к. она сводится к поиску морфологической эквивалентности подграфа схемы электрической принципиальной и графа определяемого ИС.
Критерии оптимизации при рассмотрении вопроса компоновки.
1. Минимум суммарного числа модулей, необходимых для реализации схемы
|
Xij – число модулей j-го типа i-го уровня, получается в результате компоновки схемы.
2. Минимум числа типовых скомпонованных модулей или максимальный коэффициент их повторений
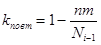 |
n - число типов модулей
m – число элементов i-го уровня в модуле
Ni-1 – общее количество элементов в i-1 уровня в схеме
3.
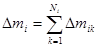 |
Минимальная избыточность в реализации
mik – число неиспользованных элементов в каждом модуле i-го уровня
4. Минимальная сумма числа внешних выводов всех модулей.
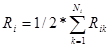 |
Rij- число внешних связей каждого модуля i-го уровня.
5. Минимальная сумма числа внешних выводов всех модулей
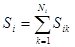 |
На задачу компоновки накладывается ряд ограничений: число элементов в типовой конструкции каждого уровня и число их выводов.
При компоновке БИС основное ограничение – площадь, отводящаяся под схему.
В точности постановку задачи компоновки формулируется как задача нелинейного целочисленного программирования:
|
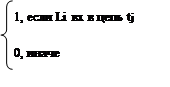 |
Элемент aij=
Необходимо скомпоновать схему в N подсхем, каждая из которых должна иметь не более Мi элементов и Кi внешних выводов, т. е. каждая электрическая схема должна входить в один типовой конструктив. Необходимо разбить множество Е элементов на L подмножеств таким образом, чтобы достигался один из критериев для всех сформированных подсхем.
Решение задачи д.б. матрица Х, состоит из элементов Хil
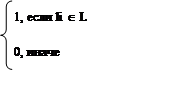 |
Xil=
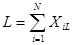 |
Количество элементов в подсхеме:
Введем целочисленную переменную Yil, которая равна 1 если J цепь соединена с элементами L –ой и какой-нибудь элемент из другой подсхемы, 0 иначе.
Количество внешних выводов L-ой подсхемы будет вычисляться как
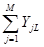 |
А суммарное количество внешних выводов всех подсхем вычисляется как
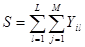 |
А число межмодульных соединений будет вычисляться следующим образом
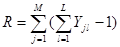 |
Такое решение задачи компоновки, в приведенной постановке, возможно только методом полного перебора, что для реализации схемы не представляет возможным даже для реальной ЭВМ, поэтому практическое применение находят приближенные алгоритмы, которые делятся на три группы последовательным алгоритмом формирования состава типовой конструкции
- Интерполяция алгоритма с последующим улучшением приближенного решения
- Смешанные.
Поиск по сайту: