Объяснение нового материала

Конспект урока информатики.

Тема: Измерение информации. Содержательный подход.

Цели урока:

· образовательная – ознакомление учащихся с понятием измерения информации, наименьшей единицей измерения информации; ознакомление с одним из подходов к измерению информации; формирования навыков решения показательных уравнений; формирование умения выделять главное из условия задачи;

· развивающие – повышение познавательного интереса к предмету;

· воспитательные – воспитание самостоятельности, ответственности, аккуратности и внимательности при выполнении заданий.

Тип урока: комбинированный

План урока:

1. организационный момент (1 мин);

2. фронтальный опрос (3 мин);

3. проверка домашнего задания (3 мин);

4. актуализация знаний (1 мин);

5. объяснение нового материала (15 мин);

6. решение задач (19);

7. постановка домашнего задания (1 мин);

8. подведение итогов урока (2 мин);

Ход урока:

Организационный момент

-Здравствуйте! Присаживайтесь

-Скажите, кто сегодня отсутствует.

Фронтальный опрос

1. Приведите свои примеры профессий, в которых основным видом деятельности является работа с информацией.

2. Назовите три основных вида информационных процессов.

3. Почему информацию, которую мы «помним наизусть», можно назвать оперативной? Приведите примеры оперативной информации, которой вы владеете.

4. Приведите примеры ситуаций, в которых вы являетесь источником информации, приемником информации. Какую роль за сегодняшний день вам чаще приходилось выполнять?

5. Приведите различные примеры процесса обработки информации. Определите, по каким правилам она производится в каждом примере

Проверка домашнего задания

Проверить наличие в тетрадях. И ученики по очереди называют ответы на вопросы.

Актуализация знаний

А теперь обсудим вопрос о том, как можно измерять информацию, Существует несколько подходов к измерению информации. Сегодня мы рассмотрим только один, который называется содержательным подходом.

Объяснение нового материала

В этом случае количество информации связывается с содержанием (смыслом) полученного человеком сообщения. Вспомним, что с «человеческой» точки зрения информация — это знания, которые мы получаем из внешнего мира. Количество информации, заключенное в сообщении, должно быть тем больше, чем больше оно пополняет наши знания.

Как же с этой точки зрения определяется единица измерения информации? Вы уже знаете, что эта единица называется «бит». Единица измерения информации была определена в науке, которая называется теорией информации. Ее определение звучит так (записать в тетрадь):

Сообщение, уменьшающее неопределенность знания в два раза, несет 1 бит информации.

Что такое неопределенность знания? Лучше всего это объяснить на примерах. Допустим, вы бросаете монету, загадывая, что выпадет: орел или решка. Есть всего два варианта возможного результата бросания монеты. Причем ни один из этих вариантов не имеет преимущества перед другим. В таком случае говорят, что они равновероятны.

Так вот, в этом случае перед подбрасыванием монеты неопределенность знания о результате равна двум. Игральный кубик с шестью гранями может с равной вероятностью упасть на любую из них. Значит, неопределенность знания о результате бросания кубика равна шести. Еще пример: спортсмены-лыжники перед забегом путем жеребьевки определяют свои порядковые номера на старте. Пусть имеется 100 участников соревнований. Тогда неопределенность знания спортсменом своего номера до жеребьевки равна 100.

Следовательно, можно сказать так (в тетрадь):

Неопределенность знания о некотором событии — это количество возможных результатов события (бросания монеты, кубика; вытаскивания жребия и пр.).

Вернемся теперь к примеру с монетой. После того как вы бросили монету и посмотрели на нее, вы получили зрительное сообщение, что выпал, например, орел. Произошло одно из двух возможных событий. В этом случае считают, что неопределенность знания уменьшилась в два раза: было два варианта, остался один. Значит, узнав результат бросания монеты, вы получили 1 бит информации.

В тетрадь:

Сообщение о том, что произошло одно событие из двух равновероятных, несет 1 бит информации.

Количество информации в сообщении об одном из N равновероятных событий

А теперь такая задача: студент на экзамене может получить одну из четырех оценок: 5 — «отлично», 4 — «хорошо», 3 — «удовлетворительно», 2 — «неудовлетворительно». Представьте себе, что ваш товарищ пошел сдавать экзамен. Причем учится он очень неровно и может с одинаковой вероятностью получить любую оценку от 2 до 5. Вы волнуетесь за него, ждете результата экзамена. Наконец, он пришел и на ваш вопрос «Ну, что получил?» ответил: «Четверку!».

Вопрос: сколько битов информации содержится в его ответе?

Если сразу сложно ответить на этот вопрос, то давайте подойдем к ответу постепенно. Будем отгадывать оценку, задавая вопросы, на которые можно ответить только «да» или «нет».

Вопросы будем ставить так, чтобы каждый ответ уменьшал количество вариантов в два раза и, следовательно, приносил 1 бит информации.

Первый вопрос:

— Оценка выше тройки?

— Да.

После этого ответа число вариантов уменьшилось в два раза. Остались только 4 и 5. Получен 1 бит информации.

Второй вопрос:

— Ты получил пятерку?

— Нет.

Выбран один вариант из двух оставшихся: оценка — четверка. Получен еще 1 бит информации. В сумме имеем 2 бита.

Сообщение о том, что произошло одно из четырех равновероятных событий, несет 2 бита информации.

Разберем еще одну частную задачу, а потом получим общее правило.

На книжном стеллаже восемь полок. Книга может быть поставлена на любую из них. Сколько информации содержит сообщение о том, где находится книга?

Будем действовать таким же способом, как в предыдущей задаче. Метод поиска, на каждом шаге которого отбрасывается половина вариантов, называется методом половинного деления. Применим метод половинного деления к задаче со стеллажом.

Задаем вопросы:

— Книга лежит выше четвертой полки?

— Нет.

— Книга лежит ниже третьей полки?

— Да.

— Книга на второй полке?

— Нет.

— Ну теперь все ясно! Книга лежит на первой полке!

Каждый ответ уменьшал неопределенность в два раза. Всего было задано три вопроса. Значит, набрано 3 бита информации. И если бы сразу было сказано, что книга лежит на первой полке, то этим сообщением были бы переданы те же 3 бита информации.

А сейчас попробуем получить формулу, по которой вычисляется количество информации, содержащейся в сообщении о том, что произошло одно из множества равновероятных событий.

Обозначим буквой N количество возможных событий. Буквой і будем обозначать количество информации в сообщении о том, что произошло одно из N событий(в тетрадь).

В примере с монетой: N = 2, і = 1.

В примере с оценками: N = 4, і = 2.

В примере со стеллажом: N = 8, і = 3.

Нетрудно заметить, что связь между этими величинами выражается такой формулой:

Действительно:

Если величина N известна, а і неизвестно, то данная формула становится уравнением для определения і. В математике оно называется показательным уравнением.

Например, пусть на стеллаже не 8, а 16 полок. Чтобы ответить на вопрос, сколько информации содержится в сообщении о том, где лежит книга, нужно решить уравнение

Поскольку 16 = 24, то і = 4.

В тетрадь:

Количество информации (і), содержащееся в сообщении о том, что произошло одно из N равновероятных событий, определяется из решения показательного уравнения .

Если значение N равно целой степени двойки (4, 8, 16, 32, 64 и т. д.), то такое уравнение решается просто: і будет целым числом. А чему, например, равно количество информации в сообщении о результате бросания игральной кости, у которой имеется шесть граней и, следовательно, N = 6? Решение уравнения

будет дробным числом, лежащим между 2 и 3, поскольку 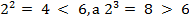. С точностью до пяти знаков после запятой решение такое: 2,58496. В учебнике приведена таблица 1.1, из которой можно определить і для различных значений N в диапазоне от 1 до 64.

Поиск по сайту: