Основы математического анализа

Теория

103. Задание {{ 17 }} 104 Тема 2-3-0

Числовая функция, определенная на множестве натуральных чисел называется бесконечной числовой...

Правильные варианты ответа: последовательностью;

104. Задание {{ 18 }} 110 Тема 2-3-0

Последовательность, имеющая предел, называется...

Правильные варианты ответа: сходящейся;

105. Задание {{ 19 }} 111 Тема 2-3-0

Последовательность, не имеющая предела, называется...

Правильные варианты ответа: расходящейся;

106. Задание {{ 20 }} 112 Тема 2-3-0

Если последовательность сходится, то она имеет только один...

Правильные варианты ответа: предел;

107. Задание {{ 21 }} 113 Тема 2-3-0

Если последовательность..., то она ограничена

Правильные варианты ответа: сходится;

108. Задание {{ 22 }} 121 Тема 2-3-0

Бесконечно малой величиной называется переменная величина,... которой равен нулю

Правильные варианты ответа: предел;

109. Задание {{ 23 }} 122 Тема 2-3-0

Переменная величина, предел которой равен нулю, называется... малой величиной

Правильные варианты ответа: бесконечно;

110. Задание {{ 24 }} 123 Тема 2-3-0

Бесконечно большой величиной называется переменная величина,... которой неограниченно возрастает по абсолютному значению

Правильные варианты ответа: предел;

111. Задание {{ 25 }} 124 Тема 2-3-0

Переменная величина, предел которой неограниченно возрастает, называется бесконечно... величиной

Правильные варианты ответа: большой;

112. Задание {{ 26 }} 125 Тема 2-3-0

... постоянной величины равен постоянной величине

Правильные варианты ответа: Предел;

113. Задание {{ 27 }} 126 Тема 2-3-0

Предел... нескольких функций равен сумме пределов этих функций

Правильные варианты ответа: суммы;

114. Задание {{ 28 }} 127 Тема 2-3-0

Предел... нескольких функций равен разности пределов этих функций

Правильные варианты ответа: разности;

115. Задание {{ 29 }} 128 Тема 2-3-0

Предел... нескольких функций равен произведению пределов этих функций

Правильные варианты ответа: произведения;

116. Задание {{ 30 }} 129 Тема 2-3-0

Предел... двух функций равен отношению предела числителя к пределу знаменателя

Правильные варианты ответа: частного;

117. Задание {{ 31 }} 139 Тема 2-3-0

Дифференциал постоянной величины равен...

Правильные варианты ответа: нулю;

118. Задание {{ 32 }} 140 Тема 2-3-0

Дифференциал... равен сумме дифференциалов

Правильные варианты ответа: суммы;

119. Задание {{ 33 }} 141 Тема 2-3-0

Дифференциал... равен разности дифференциалов

Правильные варианты ответа: разности;

120. Задание {{ 34 }} 145 Тема 2-3-0

Общее выражение всех первообразных называют... интегралом

Правильные варианты ответа: неопределенным;

121. Задание {{ 35 }} 148 Тема 2-3-0

Формулу вычисления определенного интеграла называют формулой...

Правильные варианты ответа: Ньютона-Лейбница;

122. Задание {{ 198 }} ТЗ № 198

Дополните

Если для чисел 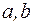при всех имеет место неравенство , то последовательность называется ###

Правильные варианты ответа: ограниченной;

124. Задание {{ 200 }} ТЗ № 200

Отметьте правильный ответ

Последовательность, заданная аналитическим выражением является

R ограниченной

£ неограниченной

£ положительной

£ отрицательной

125. Задание {{ 201 }} ТЗ № 201

Дополните

Последовательность , не являющаяся ограниченной, называется ###, если для -го члена последовательности найдется число , что .

Правильные варианты ответа: неограниченной;

126. Задание {{ 202 }} ТЗ № 202

Дополните

Если для последовательности существует число , к которому числа приближаются как угодно близко, то это число называется ### последовательности

Правильные варианты ответа: пределом;

127. Задание {{ 203 }} ТЗ № 203

Дополните

Если последовательности , ###, то

Правильные варианты ответа: сходятся;

128. Задание {{ 204 }} ТЗ № 204

Дополните

Если последовательности , ###, то

Правильные варианты ответа: сходятся;

129. Задание {{ 205 }} ТЗ № 205

Дополните

Если последовательности , ###, то

Правильные варианты ответа: сходятся;

130. Задание {{ 206 }} ТЗ № 206

Дополните

Если последовательности , ###, то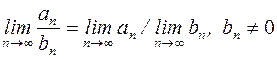

Правильные варианты ответа: сходятся;

131. Задание {{ 207 }} ТЗ № 207

Дополните

Если последовательность ###, то

Правильные варианты ответа: сходится;

132. Задание {{ 208 }} ТЗ № 208

Дополните

Функция имеет своим ### величину , если ее переменная при своем приближении к устанавливает значение функции, близкое к

Правильные варианты ответа: пределом;

133. Задание {{ 209 }} ТЗ № 209

Дополните

Запись означает, что функция имеет своим ### значение

Правильные варианты ответа: пределом;

134. Задание {{ 210 }} ТЗ № 210

Отметьте правильный ответ

Первый замечательный предел имеет вид

R

£

£

£

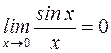
135. Задание {{ 211 }} ТЗ № 211

Дополните

Предел называется ### замечательным пределом

Правильные варианты ответа: первым;

136. Задание {{ 212 }} ТЗ № 212

Дополните

Предел называется ### замечательным пределом

Правильные варианты ответа: вторым;

137. Задание {{ 213 }} ТЗ № 213

Отметьте правильный ответ

Второй замечательный предел имеет вид

R

£

£

£

138. Задание {{ 214 }} ТЗ № 214

Отметьте правильный ответ

С помощью правила Лопиталя можно избежать неопределенности вида

R

£

£

£

139. Задание {{ 215 }} ТЗ № 215

Дополните

Формулой пользуются для вычисления производной ### функции

Правильные варианты ответа: сложной;

140. Задание {{ 216 }} ТЗ № 216

Дополните

Формулой пользуются для вычисления производной ### функции

Правильные варианты ответа: обратной;

141. Задание {{ 217 }} ТЗ № 217

Дополните

Дифференциал функции есть бесконечно малое ### функции

Правильные варианты ответа: приращение;

142. Задание {{ 218 }} ТЗ № 218

Отметьте правильный ответ

Формула приближенного вычисления имеет вид

R

£

£

£

143. Задание {{ 219 }} ТЗ № 219

Отметьте правильный ответ

Дифференциал произведения вычисляется по формуле:

R

£

£

£

144. Задание {{ 220 }} ТЗ № 220

Отметьте правильный ответ

Дифференциал частного вычисляется по формуле:

R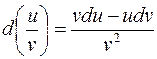

£

£

£

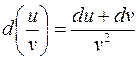
145. Задание {{ 221 }} ТЗ № 221

Отметьте правильный ответ

Дифференциал сложной функции , вычисляется по формуле

R

£

£

£

146. Задание {{ 222 }} ТЗ № 222

Отметьте правильный ответ

Формула метода подстановки для имеет вид:

R

£

£

£

147. Задание {{ 223 }} ТЗ № 223

Отметьте правильный ответ

Формула интегрирования по частям имеет вид:

R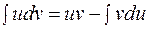

£

£

£

148. Задание {{ 224 }} ТЗ № 224

Дополните

Определенный интеграл есть ### криволинейной трапеции, ограниченной линией и прямыми

Правильные варианты ответа: площадь;

149. Задание {{ 225 }} ТЗ № 225

Дополните

Формула приближенного вычисления определенных интегралов 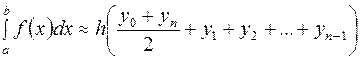называется формулой ###

Правильные варианты ответа: трапеций;

150. Задание {{ 226 }} ТЗ № 226

Дополните

Формула приближенного вычисления определенных интегралов 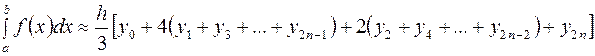называется формулой Симпсона (или ###)

Правильные варианты ответа: парабол;

Поиск по сайту: