ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Момент инерции – это физическая величина, являющаяся мерой инертности тела при его вращательном движении. В этом смысле он подобен массе, являющейся мерой инертности тела при поступательном движении. Величина момента инерции, по определению, равна сумме произведений масс частиц тела на квадраты их расстояний r до оси вращения:

J = S m _i r_i² или J = ò r ² dm. (1)

Величина момента инерции тела зависит не только от массы тела, но и от расположения частей тела относительно оси вращения. Чем дальше от оси находятся части тела, тем больше момент инерции.

Теоретический расчет момента инерции тел упрощается при применении теоремы Штейнера. Получим уравнение теоремы. Пусть точка О – центр масс тела, через которую проходит ось О – О, а параллельно ей на некотором расстоянии а ось С− С (рис. 1). Установим связь между моментами инерции тела относительно этих осей.

Представим вектор от оси С – С до некоторого элемента массы m _i как сумму векторов (рис. 1). Подставив в определяющую формулу момента инерции (1) радиус - вектор r и возведя сумму в квадрат, получим

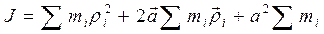. (2)

Первый член этого уравнения J ₀ – момент инерции тела относительно оси О – О, проходящей через центр масс. Во втором члене сумма определяет положение центра масс тела относительно оси О – О, и так как ось проходит через центр масс, то эта сумма равна нулю. Третий член – это произведение суммы масс частиц, то есть массы тела на квадрат расстояния между осями. Итак,

J = J ₀ + m a ². (3)

Это уравнение теоремы Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, и произведению массы тела на квадрат расстояния между осями. В тех случаях, когда момент инерции относительно оси, проходящей через центр масс J ₀ , можно сравнительно легко рассчитать, теорема Штейнера позволяет определить момент инерции относительно произвольной оси J_с, избежав весьма трудоемких расчетов.

Теорему Штейнера можно экспериментально подтвердить, если измерить момент инерции тела при разных расстояниях а от оси вращения до центра масс тела. Если зависимость J (a ²) будет линейной с угловым коэффициентом, равным массе тела, то теорема верна.

Одним из методов измерения момента инерции тел является метод крутильного маятника. Крутильный маятник – это тело, произвольной формы, подвешенное на упругих струнах. В лабораторной установке – это рамка (рис.1). Если рамку отклонить от положения равновесия и отпустить, то она под действием момента упругих сил струны (M =−kα) возвращается к положению равновесия,но по инерции проходит положение равновесия, закручивая струну в противоположном направлении. Возникают вращательные колебания. Применим основной закон динамики вращательного движения: произведение момента инерции рамки на угловое ускорение равно моменту упругих сил подвеса:

. (4)

Это дифференциальное уравнение второго порядка. Его решением должна быть функция, обращающая его в тождество. В данном случае это уравнение гармонических колебаний , где Т – период колебаний. Подставив функцию в уравнение (4), получим, что она будет решением, если период колебаний маятника равен

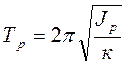. (5)

Исследуемое тело представляет собой составной цилиндр из двух половин, полуцилиндров. Наденем их на стержень на одинаковом расстоянии а (рис. 2). Момент инерции маятника изменится и будет равен сумме момента инерции рамки и искомого момента инерции цилиндра. Период тоже изменится и станет равным

. (6)

Решая совместно уравнения (5) и (6), исключая коэффициентупругости к, получим формулу для экспериментального определения момента инерции цилиндра по известному моменту инерции рамки

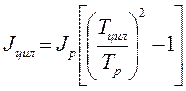. (7)

Поиск по сайту: