 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ. Колебания – это процесс движения, при котором параметры движения тела (координата, скорость, ускорение
|
Читайте также: |
Колебания – это процесс движения, при котором параметры движения тела (координата, скорость, ускорение, сила, энергия и т.д.) периодически повторяются. Колебания называются гармоническими, если смещение в зависимости от времени происходят по уравнению синуса или косинуса, например x = A cos(w t + j). Здесь А – амплитуда колебаний, то есть наибольшее смещение тела от положения равновесия, w – циклическая частота, равная числу колебаний за время 2 p секунд. Время одного полного колебания Т = 2 π / ω называется периодом колебаний. Аргумент косинуса называется фазой, j – начальная фаза.
Пусть тело участвует одновременно в двух взаимно перпендикулярных колебаниях, происходящих по уравнениям:
x = A 1cos(w 1 t + j 1), y = A 2cos (w 2 t + j 2). (1)
В общем случае траектория будет незамкнутой кривой, заполняющей прямоугольник со сторонами 2 А 1 – 2 А 2. . Лишь в том случае, когда отношение частот равно отношению целых чисел, траектория движения замыкается и периодически повторяется. Такие траектории называются фигурами Лиссажу.
Пример 1.Пусть частоты колебаний равны, w 1 = w 2, и разность фаз равна нулю: x = A 1cos(w t), y = A 2cos(w t). Чтобы найти уравнение траектории, то есть зависимость y(x), следует из уравнений исключить параметр – время t. Для этого достаточно поделить уравнения. В результате получим 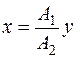 .
.
Это уравнение прямой линии, проходящей через начало координат из первого во второй квадрант (рис. 1, Δ φ = 0). Если разность фаз равна p радиан, то знак, например для координаты y, меняется и траектория колебаний проходит из второго в четвертый квадрант.
Пример 2. Пусть частоты колебаний равны, а разность фаз равна p /2. Уравнения (2) примут вид: x = A 1cos(w t), y = A 2sin(w t). Чтобы исключить время t, воспользуемся теоремой: сумма квадратов синуса и косинуса равна единице. Подставив функции синуса и косинуса, получим 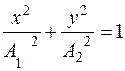 .
.
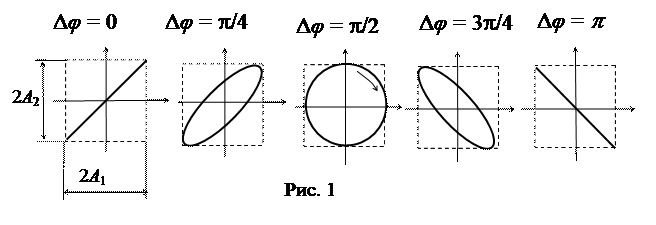
Это уравнение эллипса с полуосями А 1 и А 2. Движение по траектории начинается с точки А 1 и происходит по часовой стрелке (рис. 1, Δ φ = π/2). Если амплитуды складываемых колебаний равны, то траектория будет окружностью радиуса, равного амплитудам.
Как видно из примеров 1 и 2, при равных частотах траектория зависит от разности фаз складываемых колебаний.
Пример 3. Пусть частоты колебаний отличаются в два раза,
w2 /w1 = 2, начальные фазы равны нулю:
x = A 1cos w t, y = A 2cos2 w t. Исключим время. Подставив функции косинусов в формулу cos2 w t = 2cos 2w t – 1, получим 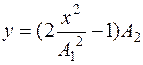 . Это уравнение параболы, вершина которой смещена по оси Оy на – А 2 (рис.2).
. Это уравнение параболы, вершина которой смещена по оси Оy на – А 2 (рис.2).
В данной работе изучение сложения взаимно перпендикулярных колебаний производится с помощью осциллографа. Если на вертикальный и горизонтальный вход осциллографа подать колебания кратных частот, то на экране можно наблюдать фигуры Лиссажу.
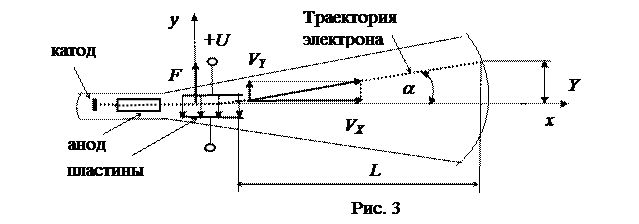 |
Осциллограф – это прибор для наблюдения быстро протекающих процессов, для измерения напряжения, частоты. Основным элементом осциллографа является электронно-лучевая трубка. Электроны, вылетающие из катода, ускоряются и фокусируются между анодом и катодом в узкий луч, который на люминесцентном экране создает светящую точку. Управление лучом производится с помощью электрического поля отклоняющих пластин (рис.3).
Когда электрон со скоростью V 0 влетает в электрическое поле вдоль пластин, то на него действует электрическая сила, перпендикулярная скорости. Она равна произведению заряда на напряженность: F= е Е. Электрон приобретает ускорение, а = еЕ/m и скорость VY = а t. Напряженность электрического поля связана с напряжением соотношением Е = U/d. Горизонтальная компонента скорости постоянна Vx= V 0, и время движения электрона в поле между пластинами длиной l равно t = l /V 0. Подставив время и ускорение в формулу для компоненты скорости VY, получим VY = 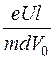 . Если пренебречь поперечным смещением луча между пластинами, то, двигаясь далее прямолинейно, он отклонится при попадании на экран Y = L tg a. Тангенс угла отклонения равен отношению компонент скорости:
. Если пренебречь поперечным смещением луча между пластинами, то, двигаясь далее прямолинейно, он отклонится при попадании на экран Y = L tg a. Тангенс угла отклонения равен отношению компонент скорости: 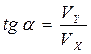 . Подставив формулы компонент скорости, получим, что смещение луча пропорционально напряжению:
. Подставив формулы компонент скорости, получим, что смещение луча пропорционально напряжению:
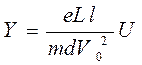 . (2)
. (2)
ВЫПОЛНЕНИЕ РАБОТЫ
1. Проверить подсоединение генераторов на вертикальный и горизонтальный входы осциллографа. Включить в сеть 220 В генераторы и осциллограф. Отключить развертку осциллографа по оси X.
| w 1 : w 2 | Разность фаз | ||
| p/2 | p | ||
| 1:1 | |||
| 1:2 | |||
| 1:3 |
2. Установить частоты генераторов в диапазоне нескольких килогерц в соотношении 1:1. Получить с помощью переключателей «Длительность» и «Усиление» на экране осциллограмму в виде прямоугольника, заполненного линиями.
3. Плавно изменяя частоту одного из генераторов в небольших пределах, добиться получения фигуры Лиссажу. Так как частота и фаза сигнала генераторов «плывет», то изображение фигуры меняется. Зарисовать фигуры Лиссажу в таблицу.
4. Повторить обнаружение фигур Лиссажу при другом соотношении частот: 1:2, 1:3…
Выключить приборы.
5. Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Запишите уравнение гармонических колебаний. Дайте определение параметрам движения.
2. Дайте определение фигур Лиссажу, условия их образования.
3. Выведите уравнение траектории при сложении колебаний одинаковой частоты с разностью фаз 0 и π/2.
4. Выведите уравнение траектории при сложении колебаний, частоты которых отличаются в 2 раза.
5. Объясните принцип работы осциллографа.
6. Докажите, что смещения электронного луча на экране пропорционально напряжению на входе Y осциллографа.
Работа 13
Поиск по сайту: