 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ФИЗИЧЕСКОГО МАЯТНИКА
Цель работы: определить момент инерции физического маятника в виде стержня с грузами по периоду собственных колебаний.
Оборудование: маятник, секундомер.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Момент инерции твердого тела – это мера инертности тела при его вращательном движении. В этом смысле он является аналогом массы тела, которая является мерой инертности тела при поступательном движении. Согласно определению, момент инерции тела равен сумме произведений масс частиц тела mi на квадраты их расстояний до оси вращения ri 2:
, или 
.(1)
Момент инерции зависит не только от массы, но и от ее распределения относительно оси вращения. Как видно, инертность при вращении тела тем больше, чем дальше от оси расположены частицы тела.
Существуют различные экспериментальные методы определения момента инерции тел. В работе предлагается метод определения момента инерции по периоду собственных колебаний исследуемого тела как физического маятника. Физический маятник – это тело произвольной формы, точка подвеса которого расположена выше центра тяжести. Если в поле тяжести маятник отклонить от положения равновесия и отпустить, то под действием силы тяжести маятник стремится к положению равновесия, но, достигнув его, по инерции продолжает движение и отклоняется в противоположную сторону. Затем процесс движения повторяется в обратном направлении. В итоге маятник будет совершать вращательные собственные колебания.
Для вывода формулы периода собственных колебаний применим основной закон динамики вращательного движения. Угловое ускорение тела прямо пропорционально моменту силы и обратно пропорционально моменту инерции тела относительно оси вращения:
e = 
. (2)
 |
Момент силы по определению равен произведению силы на плечо силы. Плечо силы – это перпендикуляр, опущенный из оси вращения на линию действия силы. Для маятника (рис. 1а) плечо силы тяжести равно d = а sin a, где а – расстояние между осью вращения и центром тяжести маятника. При малых колебаниях маятника угол отклонения a сравнительно мал, а синусы малых углов с достаточной точностью равны самим углам. Тогда момент силы тяжести можно определить по формуле М=−mgа∙a. Знак минус обусловлен тем, что момент силы тяжести противодействует отклонению маятника.
Так как угловое ускорение – это вторая производная от угла поворота по времени, то основной закон динамики вращательного движения (1) принимает вид
. (3)
Это дифференциальное уравнение второго порядка. Его решением должна быть функция, превращающая уравнение в тождество. Такой функцией может быть функция синуса
a = a 0sin(w t + j). (4)
При этом циклическая частота равна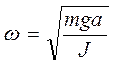 
. Циклическая частота связана с периодом колебаний, то есть временем одного колебания, соотношением T = 2 p /w. Отсюда
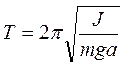. (5)
Период колебаний Т и расстояние от оси вращения до центра тяжестимаятника а измерить можно. Тогда из (5) момент инерции маятника относительно оси вращения С может быть определен экспериментально по формуле
. (6)
Маятник, момент инерции которого определяется в работе, представляет собой стержень с надетыми на него двумя дисками. Теоретически момент инерции маятника можно определить как сумму моментов инерции отдельных частей. Момент инерции дисков можно рассчитать по формуле момента инерции материальной точки, так как они невелики по сравнению с расстоянием до оси вращения: 
, 
. Момент инерции стержня относительно оси, находящейся на расстоянии b от середины стержня, можно определить по теореме Штейнера 
. В итоге суммарный момент инерции маятника можно рассчитать по формуле
. (7)
Здесь m 1, m 2 и m 0 – массы первого, второго дисков и стержня, l 1, l 2 – расстояния от середин дисков до оси вращения, l 0 – длина стержня.
Расстояние от точки подвеса до центра тяжести маятника а, необходимое для определения момента инерции в формуле (6), можно определить экспериментально, используя понятие центра тяжести. Центр тяжести тела – это точка, к которой приложена равнодействующая сила тяжести. Поэтому если маятник положить горизонтально на опорную призму, расположенную под центром тяжести, то маятник будет в равновесии. Затем достаточно измерить расстояние от оси С до опорной призмы.
Но можно определить расстояние а расчетом. Из условия равновесия маятника на призме (рис. 1б) следует, что момент результирующей силы тяжести относительно оси С равен сумме моментов сил тяжести грузов и стержня: (m 1 +m 2 + m 0) gа = m 1 gl 1 + m 2 gl 2 + m 0 gb. Откуда получим
. (8)
ВЫПОЛНЕНИЕ РАБОТЫ
1. Взвешиванием на весах определить массы дисков и стержня. Расположить на стержне и закрепить диски. Измерить расстояния от оси вращения до середин дисков l 1, l 2 и до середины стержня b, длину стержня l 0 по сантиметровым делениям на стержне. Результаты измерений записать в табл. 1.
Включить установку в сеть 220 В, нажать кнопку «Сеть».
Таблица 1
| Масса 1го диска m 1, кг | |
| Масса 2го диска m 2, кг | |
| Масса стержня m 0, кг | |
| Расстояние l 1, см | |
| Расстояние l 2, см | |
| Длина стержня l 0, см | |
| Расстояние до оси b, см |
2. Измерить период колебаний. Для этого отвести маятник от положения равновесия на небольшой угол и отпустить. Нажать кнопку «Пуск» секундомера. Чтобы измерить время t, например, десяти колебаний, следует после девятого колебания нажать кнопку «Стоп». Период равен Т= t/ 10. Записать результат в табл. 2, нажать кнопку «Сброс». Опыт повторить еще не менее трех раз при других углах отклонения.
Выключить установку.
3. Произвести расчеты в системе СИ. Определить среднее значение < Т > периода колебаний. Определить расстояние а от оси до центра тяжести маятника по формуле (8), или положить маятник на опорную призму так, чтобы он находился в равновесии, и по делениям на стержне измерить расстояние а.
4. Определить экспериментальное среднее значение момента инерции маятника < Jэкс > по формуле (6) по среднему значению периода колебаний < T >.
Таблица 2
| а, м | Т 1, с | Т 2, с | Т 3, с | < T >,с | <Jэксп>, кг∙м2 | Jтеор, кг∙м2 |
5. Определить теоретическое значение момента инерции маятника Jтеор по формуле (7).
6. Сделать вывод, сравнив теоретическое и экспериментальное значения момента инерции маятника. Оценить погрешность измерения D J =<J эксп> – J теор.
7. Записать ответ в виде: Jэксп = < J > ±D J.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение физического маятника, объясните, почему возможны собственные колебания маятника.
2. Запишите основной закон динамики вращательного движения для физического маятника.
3. В каком виде ищут функцию, являющуюся решением дифференциального уравнения динамики для физического маятника. Проверьте, будет ли эта функция решением.
4. Запишите формулу для периода колебаний физического маятника. Как изменится период колебаний, если нижний диск сместить еще ниже?
5. Дайте определение момента инерции. Выведите формулу для определения теоретического значения момента инерции маятника.
6. Дайте определение центра тяжести. Выведите формулу для расчета положения центра масс. Как экспериментально можно определить положение центра масс маятника?
Работа 14
Поиск по сайту: