 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ИЗУЧЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Цель работы: проверить выполнение основного закона динамики вращательного движения, определить момент инерции маятника Обербека.
Оборудование: маятник Обербека, секундомер, грузы.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Вращательное движение тела вокруг неподвижной оси – это движение, при котором траектории всех точек тела являются концентрическими окружностями, центры которых лежат на линии, являющейся осью вращения. Параметрами вращательного движения тела являются: угловой путь j, то есть угол поворота тела вокруг оси; угловая скорость w = 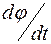 ; и угловое ускорение e =
; и угловое ускорение e = 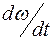 . Это аксиальные векторы, то есть векторы, направленные по оси вращения. Если вращать буравчик вместе с телом, то направление его поступательного движения вдоль оси совпадает с вектором угловой скорости.
. Это аксиальные векторы, то есть векторы, направленные по оси вращения. Если вращать буравчик вместе с телом, то направление его поступательного движения вдоль оси совпадает с вектором угловой скорости.
Угловое ускорение тела ε, согласно основному закону динамики вращательного движения, прямо пропорционально моменту силы M, действующему на тело,и обратно пропорционально моменту инерции тела относительно оси:
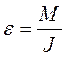 . (1)
. (1)
 Момент силы по определению – это вектор, равный векторному произведению радиус-вектора точки приложения силы на вектор
Момент силы по определению – это вектор, равный векторному произведению радиус-вектора точки приложения силы на вектор
силы: 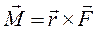 . Величину проекции вектора момента силы на ось вращения можно определить как произведение величины силы на ее плечо:
. Величину проекции вектора момента силы на ось вращения можно определить как произведение величины силы на ее плечо:
М = F d. (2)
Плечо силы d – это длина перпендикуляра, опущенного из оси вращения на линию действия силы. Направление вектора момента силы относительно оси также определяется правилом буравчика: это аксиальный вектор, направленный в сторону поступательного движения буравчика под воздействием сил, действующих на ручки.
Момент инерции по определению – это скалярная физическая величина, равная сумме произведений масс частиц тела mi (или dm)на квадраты их расстояний r до оси вращения:
J = å m i r i 2, или 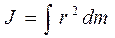 . (3)
. (3)
Физический смысл момента инерции можно установить по уравнению (1). Это мера инертности тела при вращательном движении. Чем больше момент инерции тела, тем меньше его угловое ускорение при действии того же момента сил. В этом смысле он является аналогом массы, являющейся мерой инертности тела при поступательном движении. Но момент инерции зависит не только от массы, но и от ее распределения. Чем дальше от оси вращения находятся части тела, тем больше момент инерции, тем меньше угловое ускорение, тем медленнее раскручивается или тормозит вращающееся тело.
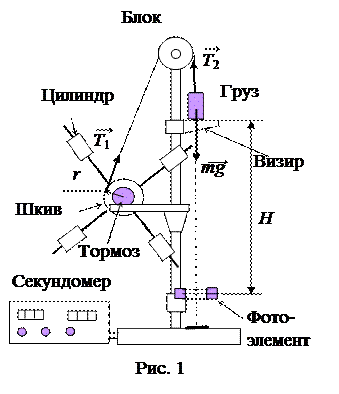 Изучение закономерностей вращательного движения в работе производится с помощью маятника Обербека (рис.1). Он представляет собой крестовину, которая может вращаться вокруг оси. На спицах крестовины расположены цилиндры. На шкив маятника наматывается нить, на конце которой подвешен груз массы m. Вращение крестовины происходит под воздействием момента силы натяжения нити
Изучение закономерностей вращательного движения в работе производится с помощью маятника Обербека (рис.1). Он представляет собой крестовину, которая может вращаться вокруг оси. На спицах крестовины расположены цилиндры. На шкив маятника наматывается нить, на конце которой подвешен груз массы m. Вращение крестовины происходит под воздействием момента силы натяжения нити 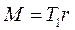 , где r – радиус шкива, являющийся плечом силы натяжения.
, где r – радиус шкива, являющийся плечом силы натяжения.
Для подтверждения основного закона динамики вращательного движения (1) следует независимо определить момент силы натяжения нити и угловое ускорение крестовины маятника и убедиться в том, что они пропорциональны друг другу. Коэффициент пропорциональности равен величине, обратной моменту инерции 1/ J.
Силу натяжения нити Т 1 =Т 2 определим из уравнения второго закона Ньютона для груза, движущегося под действием силы тяжести mg и силы натяжения нити:
m a = mg – T 2. (4)
Откуда T 2 = m (g –a). Тогда момент силы натяжения нити можно рассчитать по формуле M = m (g – a) r. В лабораторной установке ускорение падения груза много меньше ускорения свободного падения, a<<g. Поэтому момент силы, вращающий крестовину, можно определить достаточно точно по приближенной формуле
M = mgr. (5)
Угловое ускорение e крестовины связано с тангенциальным ускорением точек поверхности шкива радиусом соотношением a = e r. Такое же ускорение имеет груз. Для экспериментального определения ускорения груза применим уравнение кинематики равноускоренного движения 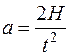 . Тогда угловое ускорение крестовины можно определить по формуле
. Тогда угловое ускорение крестовины можно определить по формуле
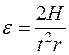 , (6)
, (6)
 где Н – высота падения груза; t – время падения; r – радиус шкива.
где Н – высота падения груза; t – время падения; r – радиус шкива.
Основной закон динамики будет подтвержден, если на построенном графике зависимости углового ускорения крестовины от момента силы экспериментальные точки будут близко расположены относительно линии прямо пропорциональной зависимости.
На самом деле существует момент сил трения в подшипниках оси, и экспериментальная прямая будет смещена по оси абсцисс на величину момента сил трения. Однако угловой коэффициент теоретической и экспериментальной линий будет одинаков. Это позволяет определить среднее значение момента инерции крестовины графическим методом как
отношение катетов прямоугольного треугольника, построенного на экспериментальной линии как на гипотенузе (рис. 2):
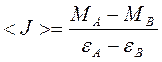 . (7)
. (7)
ВЫПОЛНЕНИЕ РАБОТЫ
1. Убедиться, что крестовина сбалансирована и не вращается при ненатянутой нити. При необходимости сместить цилиндры на спицах и закрепить. Установить визир на некоторой высоте. Измерить высоту H падения груза по шкале как расстояние между визиром и лучом фотоэлемента. Измерить радиус одного из шкивов r. Измерить расстояние от оси до цилиндров l. Результаты записать в табл. 1.
Таблица 1 Таблица 2
| Высота падения Н, см | |
| Радиус шкива r, мм | |
| Расстояние до цилиндров l, см |
| m, г | t, c | e, рад/с | M, Н∙м |
2. Установить наименьший груз, определить его массу. Намотать нить на выбранный шкив, вращая крестовину, так чтобы дно груза оказалось на уровне визира. Включить установку в сеть 220 В.
Нажать кнопку «Сеть» (на задней панели), при этом будет включен электромагнитный тормоз. Нажать кнопку «Пуск». Тормоз отпустит крестовину, начнется счет времени секундомером. В момент перекрытия грузом луча фотоэлемента счет прекратится, тормоз остановит вращение. Записать массу груза и время падения в табл. 2. Выключить секундомер кнопкой «Сеть» для отключения тормоза.
3. Вращая крестовину, снова поднять груз к визиру. Снова включить секундомер кнопкой «Сеть». Повторить измерения времени падения груза не менее шести раз, увеличивая разновесами массу груза до наибольшей. Записать суммарную массу грузов и время падения в каждом опыте в табл.2.
Выключить установку.
4. Произвести расчеты в системе СИ. Определить по формулам (5) и (6) угловое ускорение крестовины e и момент силы натяжения нити М в каждом опыте. Результаты записать в табл. 2.
5. Построить график зависимости углового ускорения крестовины от момента силы натяжения. Размер графика не менее половины страницы, на осях координат указать равномерный масштаб. Провести около точек прямую линию так, чтобы отклонения точек от экспериментальной линии были минимальны.
6. Построить на экспериментальной линии как на гипотенузе прямоугольный треугольник (рис. 2). По координатам вершин треугольника А и В по формуле (7) рассчитать среднее значение момента инерции < J >.
7. Оценить случайную погрешность измерения графическим методом (рис. 2) по формуле
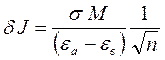 . (8)
. (8)
8. Записать результат в виде J = < J > ± d J, Р = 0,90. Оценить разумность результата, сравнив его среднее значение по порядку величины с расчетным значением момента инерции четырех цилиндров
Jцил = 4 mцил l 2 . Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте основной закон динамики вращательного движения.
2. Дайте определение момента силы. Чему равен момент силы, действующий на крестовину маятника?
3. Дайте определение момента инерции, каков его физический смысл? От чего зависит момент инерции?
4. Как изменится момент инерции, угловое ускорение крестовины, если цилиндры на спицах сместить ближе к оси?
5. От каких параметров зависит угол наклона экспериментальной линии на графике e (M)?
6. Как изменится момент силы натяжения и угловое ускорение крестовины при увеличении массы груза в чашке?
Работа 5
Поиск по сайту: