 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ИССЛЕДОВАНИЕ ДВИЖЕНИЯ ТЕЛ В ПОЛЕ ТЯЖЕСТИ
Цель работы: определить ускорение свободного падения тел в поле тяжести с помощью машины Атвуда.
Оборудование: машина Атвуда, секундомер, фотоэлемент.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
 В поле тяжести около поверхности Земли, при отсутствии сил сопротивления, тела падают с ускорением свободного падения, которое не зависит от массы тела. Действительно, в уравнении второго закона Ньютона для свободно падающего тела
В поле тяжести около поверхности Земли, при отсутствии сил сопротивления, тела падают с ускорением свободного падения, которое не зависит от массы тела. Действительно, в уравнении второго закона Ньютона для свободно падающего тела 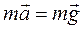 масса сокращается, потому что сила тяжести пропорциональна массе тела. На уровне моря ускорение свободного падения равно 9,81 м/с2. Это сравнительно большое ускорение и непосредственное измерение по падению тел с некоторой высоты связано с погрешностью измерения малых промежутков времени падения, с неучетом сил сопротивления. Определить ускорение свободного падения можно с помощью машины Атвуда, в которой времена движения грузов сравнительно большие, можно учесть силы сопротивления.
масса сокращается, потому что сила тяжести пропорциональна массе тела. На уровне моря ускорение свободного падения равно 9,81 м/с2. Это сравнительно большое ускорение и непосредственное измерение по падению тел с некоторой высоты связано с погрешностью измерения малых промежутков времени падения, с неучетом сил сопротивления. Определить ускорение свободного падения можно с помощью машины Атвуда, в которой времена движения грузов сравнительно большие, можно учесть силы сопротивления.
Машина представляет собой стойку, на вершине которой расположен легкий блок (рис.1). Через блок переброшена тонкая нить, на концах которой висят два одинаковых груза массами m 0. Положим на груз над фотоэлементом перегрузок массой Δ m. Система грузов в этом случае выходит из равновесия и начинает двигаться с постоянным ускорением под действием вертикальных сил тяжести и сил натяжения нитей.
Более тяжелый груз (с перегрузком) движется ускоренно вниз. Уравнение второго закона Ньютона для него в проекции на ось, направленную вертикально вниз, имеет вид
 . (1)
. (1)
Второй груз под действием силы натяжения нити движется вверх с таким же ускорением (если нить нерастяжима). В проекции на вертикальную ось, направленную вверх, уравнение второго закона Ньютона примет вид
 . (2)
. (2)
При очень легком блоке, когда можно пренебречь инертностью вращения блока и трением в оси, силы натяжения по обе стороны блока были бы равны друг другу: Т 1 = Т 2. Однако, для повышения точности измерений учтем эти факторы, введя уравнение динамики вращательного движения блока: произведение момента инерции блока на угловое ускорение равно алгебраической сумме моментов сил натяжения и трения
 . (3)
. (3)
Угловое ускорение блока связано с касательным ускорением соотношением  , а момент сил трения в оси блока и сил сопротивления воздуха заменим произведением эквивалентной силы трения на радиус блока
, а момент сил трения в оси блока и сил сопротивления воздуха заменим произведением эквивалентной силы трения на радиус блока  . Будем считать блок однородным диском, для которого момент инерции равен
. Будем считать блок однородным диском, для которого момент инерции равен  . Сложим уравнения (1), (2) и (3) с учетом указанных соотношений, и получим уравнение движения тел
. Сложим уравнения (1), (2) и (3) с учетом указанных соотношений, и получим уравнение движения тел
 ,
,
или  , (3)
, (3)
где  – суммарная эффективная масса движущихся тел машины, Δ m – масса перегрузка.
– суммарная эффективная масса движущихся тел машины, Δ m – масса перегрузка.
Ускорение а движения грузов можно определить экспериментально по времени движения некоторого расстояния S, используя формулы кинематики равноускоренного движения
 , или
, или  . (4)
. (4)
Однако в уравнении (3) для определения ускорения свободного падения остается неизвестной еще величина силы трения. Чтобы ее исключить, проведем несколько опытов с различным значением массы перегрузка Δ m. Если построить по результатам измерений график зависимости левой части уравнения (3) от массы перегрузка, то угловой коэффициент экспериментальной линии будет равен искомому значению ускорения свободного падения, а отрезок, отсекаемой линией на отрицательном участке оси ординат будет равен силе трения (рис. 2).
 Для определения углового коэффициента экспериментальной линии построим на линии как на гипотенузе прямоугольный треугольник, по возможности крупнее. Угловой коэффициент будет равен отношению катетов треугольника. По координатам вершин треугольника среднее значение ускорения свободного падения будет равно
Для определения углового коэффициента экспериментальной линии построим на линии как на гипотенузе прямоугольный треугольник, по возможности крупнее. Угловой коэффициент будет равен отношению катетов треугольника. По координатам вершин треугольника среднее значение ускорения свободного падения будет равно
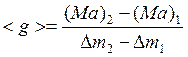 . (5)
. (5)
ВЫПОЛНЕНИЕ РАБОТЫ
1. Установить одинаковые исходные массы обоих грузов m 0. Положить перегрузок Δ m на груз, который движется на фотоэлемент. Определить эффективную суммарную массу тел  . Записать массу перегрузка Δ m и суммарную массу тел М в таблицу.
. Записать массу перегрузка Δ m и суммарную массу тел М в таблицу.
2. Повесить нить с грузами на блок. Установить фотоэлемент в нижнем положении на стойке. Проверить, достаточна ли длина нитей, опускается ли тяжелый груз в центр фотоэлемента. Измерить высоту падения S тяжелого груза как расстояние от визира до луча фотоэлемента. Записать в таблицу.
Включить установку в сеть 220 В.
3. Поднять тяжелый груз в верхнее положение так, чтобы донышко груза было на уровне визира. Нажать кнопку «Сеть» (на задней панели), и электромагнитный тормоз будет удерживать грузы. Нажать кнопку «Пуск» секундомера. Грузы придут в движение, секундомер начнет счет времени. В момент перекрытия грузом луча фотоэлемента счет прекратится, включится тормоз. Записать в таблицу время падения t. Выключить секундомер кнопкой «Сеть»
4. Поднять тяжелый груз в исходное состояние к визиру и снова включить секундомер кнопкой «Сеть». Повторить измерения времени падения груза не менее пяти раз, добавляя дополнительные перегрузки. Записать в таблицу суммарную массу тел, массу перегрузков и время падения в каждом опыте.
Выключить установку.
| S, см | |||||
| Δ m, г | |||||
| М, г | |||||
| t, с | |||||
| а, м/c2 | |||||
| Ма, Н |
5. Произвести расчеты. При расчетах перевести измеренные значения в систему СИ. Определить ускорение движения грузов по формуле  . Записать в таблицу.
. Записать в таблицу.
6. Построить график зависимости Ма (Δ m)размером не менее половины страницы. На осях координат указать равномерный масштаб. Около точек провести прямую линию так, чтобы отклонения точек были минимальными.
7. Определить среднее значение ускорения падения груза как угловой коэффициент экспериментальной линии. Для этого на линии как на гипотенузе построить прямоугольный треугольник с вершинами 1 и 2 на концах линии (рис. 2). Среднее значение ускорения свободного падения, согласно формуле (5), будет равно отношению катетов треугольника.
8. Оценить случайную погрешность измерения ускорения свободного падения по формуле
 , (6)
, (6)
где n – число измерений, σ (Ма) – расстояние между вспомогательными линиями на рис. 2.
9. Записать результат измерения в виде 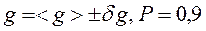 .
.
Сравнить с табличным значением, сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Перечислите факторы, от которых зависит ускорение свободного падения.
2. Объясните преимущества машины Атвуда по сравнению с прямым измерением ускорения падающих тел.
3. Выведите формулу для экспериментального определения ускорения свободного падения с помощью машины Атвуда.
4. Объясните графический способ определения ускорения свободного падения. Почему необходим графический способ?
5. Как можно определить эквивалентную силу сопротивления движению с помощью графика Ma (Δ m)?
6. Как влияет на результат измерения ускорения свободного падения сила трения в установке и инертность блока?
Поиск по сайту: