 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ВЫПОЛНЕНИЕ РАБОТЫ
1. Определить взвешиванием на весах массы обоих шаров. Результат записать в табл. 1.
Таблица 1
| Масса правого шара m 1, кг | |
| Масса левого шара m 2, кг | |
| Отклонение правого шара b 1, рад |
2. Произвести не менее шести опытов по упругому удару шаров. Для этого шары отвернуть пластилиновой нашлёпкой от точки удара.
Отвести правый шар вдоль шкалы на некоторый, одинаковый во всех опытах, угол и измерить угол отклонения β 1. Отпустить шар. Убедиться, что шары после удара движутся вдоль шкалы. Поймать левый шар после удара в его крайнем положении, чтобы не допустить второго удара. Измерить углы отклонения γ 1 и γ 2. Положительное значение угла γ 1 отсчитывается по правой шкале, угла γ 2 – по левой. Результаты записать в табл. 2.
3. Произвести не менее шести опытов по неупругому удару. Для этого шары повернуть пластилиновой нашлёпкой к точке удара. Отвести правый шар на угол b 1. Угол отклонения шаров после удара при их совместном движении γ 12 измерить по отклонению левого шара по левой шкале. Результаты записать в табл. 2.
Таблица 2
| Упругий удар | ||||||||
| g1 ∙10-2, рад | <g 1> = | |||||||
| g2 ∙10-2, рад | <g2> = | |||||||
| Неупругий удар | ||||||||
| g12 ∙10-2, рад | <g12> = |
4. Провести обработку результатов измерений. Определить среднее арифметическое значение углов отклонения шаров после удара: <γ 1 >, <γ 2 >, <g 12 >. Записать в табл. 2.
5. Рассчитать левые и правые части уравнений (6) и (7) по значениям масс шаров и средним значениям углов отклонения. Убедиться в их приближенном равенстве. Записать в табл. 3.
6. Определить экспериментальное значение коэффициентов восстановления энергии по формулам (8) и (9) для упругого и неупругого ударов по средним значениям углов отклонения шаров. Записать в табл. 3. Сравнить с теоретическим значением, рассчитанным по формуле (10) для неупругого удара и для упругого удара Купр = 1.
Таблица 3
| Упругий удар | Неупругий удар | ||
m 1 β 1 = 
| Купр | m 1 β 1 = 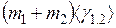
| Кнеупр |
7. Оценить относительную погрешность выполнения закона сохранения импульса, например для неупругого удара, по формуле
 . (11)
. (11)
Сделать вывод о выполнении закона сохранения импульса.
8. Оценить относительную погрешность измерения коэффициента восстановления энергии по формуле ε = 1 – К упр. Сделать вывод о сохранении механической энергии при упругом ударе.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение импульса тела и импульса силы. Объясните на основании второго закона Ньютона возникновение больших сил при кратковременном ударе.
2. Сформулируйте закон сохранения импульса и условия для выполнения удара тел.
3. Дайте определение упругого и неупругого ударов. Какие происходят при этом процессы превращения энергии.
4. Как будут двигаться одинаковые шары после упругого и неупругого ударов, если: а) до удара они двигались навстречу; б) один из шаров покоился?
5. Выведите формулу скорости шара в зависимости от угла отклонения шара от положения равновесия.
6. Дайте определение коэффициента восстановления энергии. Выведите формулу для коэффициента восстановления при неупругом ударе шаров. В каких случаях коэффициент К= 1 или К= 0?
Работа 2
ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ
БАЛЛИСТИЧЕСКИММЕТОДОМ
Цель работы: познакомиться с баллистическим методом определения скорости пули, с применением законов сохранения импульса и энергии.
Оборудование: пружинный пистолет, пуля, баллистический маятник, шкала.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
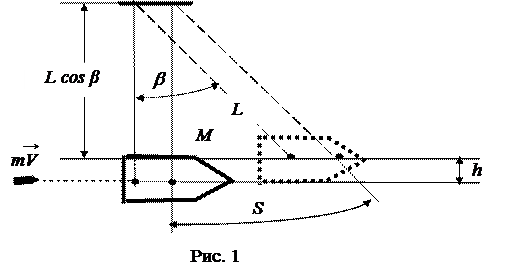
Баллистический метод измерения скорости пули основан на том, что отклонение баллистического маятника после удара пули пропорционально ее скорости. Баллистический маятник представляет собой массивную мишень, подвешенную на нитях (рис. 1). Летящая пуля попадает в мишень, происходит удар и пуля застревает в мишени. Мишень отклоняется.
Существуют две идеализации реального удара: идеально упругий удар и абсолютно неупругий удар. При абсолютно неупругом ударе деформация тел пластическая и удар заканчивается на фазе сближения, после чего тела движутся совместно. Совместное движение тел после удара является признаком абсолютно неупругого удара. При неупругом ударе кинетическая энергия частично превращается во внутреннюю энергию и в результате не сохраняется. Удар пули о мишень можно считать абсолютно неупругим ударом.
Из-за кратковременности взаимодействия тел при ударе возникают сравнительно большие внутренние ударные силы.
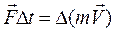 . Тогда при
. Тогда при  . Так что внешними силами при ударе можно пренебречь и считать систему соударяющихся тел замкнутой. В этом случае выполняется закон сохранения импульса: в замкнутой системе тел сумма импульсов тел постоянна, или сумма импульсов тел до взаимодействия равна сумме импульсов тел после взаимодействия:
. Так что внешними силами при ударе можно пренебречь и считать систему соударяющихся тел замкнутой. В этом случае выполняется закон сохранения импульса: в замкнутой системе тел сумма импульсов тел постоянна, или сумма импульсов тел до взаимодействия равна сумме импульсов тел после взаимодействия:
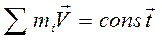
|
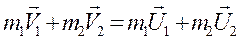 . (1)
. (1)
Для процесса неупругого удара пули о мишень закон сохранения импульса в проекции на ось Ох примет вид
mV = (m + M) U. (2)
 |
То есть импульс пули до удара равен импульсу мишени с застрявшей пулей после удара. Здесь m, V – масса и скорость пули до удара, М – масса мишени, U – скорость мишени с застрявшей пулей после удара.
Приобретя скорость, мишень с пулей отклоняются по дуге окружности S, поднимаясь на некоторую высоту h (рис. 1). Для процесса подъема можно применить закон сохранения механической энергии: в замкнутой системе тел, силы взаимодействия между телами которой являются консервативными, механическая энергия постоянна, или механическая энергия тел до процесса взаимодействия равна их механической энергии после процесса. Рассмотрим правомерность применения закона. Во-первых, мишень с пулей и Земля являются замкнутой системой тел. Во-вторых, действующие между ними силы тяжести и упругости нитей подвеса являются консервативными. Поэтому
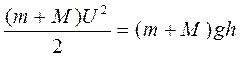 . (3)
. (3)
То есть кинетическая энергия, которую приобрела мишень после удара пули, переходит по мере подъема в поле тяжести в потенциальную энергию мишени с пулей. Здесь h – наибольшая высота подъема мишени.
Вместо высоты h удобнее измерять смещение мишени по шкале S. Выразим высоту подъема через смещение по дуге окружности S (рис. 1). Высота подъема при отклонении мишени h = L – L cos b, где L – длина нити. При малых углах отклонения мишени функцию косинуса можно приближенно определить как сумму двух членов разложения в ряд: cos b = 1 −b 2 / 2. Тогда высота подъема через угол отклонения будет: h = L b 2 / 2. Угол b является центральным углом для дуги S и связан с ней соотношением S = Lb. Таким образом, высота подъема мишени может быть определена через смещение мишени формулой
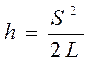 . (4)
. (4)
Решая совместно уравнения (2), (3) и (4), получим для скорости пули формулу
 . (5)
. (5)
Установка для изучения баллистического метода измерения скорости пули представляет собой мишень, подвешенную на нитях, и пружинного пистолета. Смещение мишени S после выстрела определяется по шкале.
ВЫПОЛНЕНИЕ РАБОТЫ
1. Определить массу пули m взвешиванием на весах. Массу пули и параметры установки записать в табл. 1.
Таблица1
| Масса мишени М, кг | |
| Масса пули m, кг | |
| Длина подвеса L, м |
2. Взвести пружинный пистолет, зарядить пулей и произвести пробный выстрел. Убедиться, что пуля попадает в мишень, и она отклоняется вдоль шкалы. При необходимости произвести регулировку длины нитей подвеса.
3. Произвести не менее шести раз выстрелы и измерить каждый раз смещение мишени S по шкале. Результаты записать в табл. 2.
Таблица 2
| S, м | < S >, м = |
4. Произвести обработку результатов измерений. Определить среднее арифметическое отклонение мишени < S >. Записать в табл. 2. Определить по формуле (5) среднее значение скорости пули по среднему значению отклонения мишени <S>.
5. Оценить случайную погрешность измерения скорости пули, считая, что она обусловлена в основном случайной погрешностью измерения отклонения мишени после выстрела δS по формуле
 , где
, где 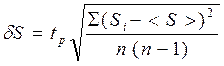 . (6)
. (6)
Убедиться, что систематической погрешностью измерения скорости пули можно пренебречь.
6. Записать результат работы в виде V = <V> ± d V, P = 0,90. Проверить, достаточно ли разумен результат.
Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение импульса тела, сформулируйте закон сохранения импульса и условия его выполнения.
2. Запишите закон сохранения импульса для процесса неупругого удара пули о мишень.
3. Дайте определение консервативных и диссипативных сил. Приведите примеры.
4. Дайте определение кинетической и потенциальной энергий. Сформулируйте закон сохранения механической энергии и условия его выполнения.
5. Запишите закон сохранения механической энергии для процесса отклонения мишени с пулей после удара пули в поле тяжести.
6. Выведите формулу для расчета скорости пули через смещение мишени после удара.
Поиск по сайту: