 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Цель работы: изучить закономерности затухающих колебаний, определить параметры затухания, коэффициент трения качения.
Оборудование: маятник (шарик на нити), наклонная плоскость, шкала, секундомер.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Маятники – это тела, которые при выведении их из положения устойчивого равновесия совершают после этого собственные колебания под действием внутренней возвращающей силы. Например, для пружинного маятника это силы упругости. Эти силы в первом приближении пропорциональны смещению х от равновесия  где
где 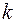 – коэффициент упругости. Реально собственные колебания маятников всегда затухающие из-за сопротивления среды. Примем, что сила сопротивления пропорциональна скорости
– коэффициент упругости. Реально собственные колебания маятников всегда затухающие из-за сопротивления среды. Примем, что сила сопротивления пропорциональна скорости 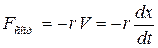 . Так бывает при движении тела в вязкой среде с небольшой скоростью.
. Так бывает при движении тела в вязкой среде с небольшой скоростью.
Получим уравнение затухающих колебаний. Уравнениевторого закона Ньютонав проекции на ось Ох будет иметь вид: произведение массы тела на ускорение равно сумме проекций сил упругости и сопротивления:
 . (1)
. (1)
Приведём это уравнение к канонической форме, поделив его на массу
 . (2)
. (2)
Здесь обозначено: 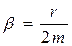 – коэффициент затухания,
– коэффициент затухания,  – циклическая частота свободных (незатухающих) колебаний.
– циклическая частота свободных (незатухающих) колебаний.
Решением этого дифференциального уравнения является функция, превращающая уравнение в тождество
 , (3)
, (3)
где  – циклическая частота затухающих колебаний,
– циклическая частота затухающих колебаний,  – амплитуда колебаний в начальный момент времени,
– амплитуда колебаний в начальный момент времени,  – начальная фаза колебаний. При малом затухании (b << w0) частота затухающих колебаний практически не отличается от частоты свободных колебаний. Если b > w0, то колебания невозможны.
– начальная фаза колебаний. При малом затухании (b << w0) частота затухающих колебаний практически не отличается от частоты свободных колебаний. Если b > w0, то колебания невозможны.
 Амплитудой затухающих колебаний является выражение перед синусом в уравнении (3)
Амплитудой затухающих колебаний является выражение перед синусом в уравнении (3)
А =А 0 е -b t. (4)
Как видно, со временем амплитуда уменьшается по экспоненциальному закону (рис.1, пунктир).
Затухание колебаний характеризуют несколькими параметрами. Во-первых, коэффициент затухания, который характеризует уменьшение амплитуды со временем, согласно формуле (4). Пусть за некоторое время τ, называемое временем релаксации, амплитуда уменьшилась в e = 2,72 раза, тогда  , откуда
, откуда  . То есть коэффициент затухания равен величине, обратной времени релаксации.
. То есть коэффициент затухания равен величине, обратной времени релаксации.
Во-вторых, параметром затухания является логарифмический декремент. По определению он равен логарифму отношения амплитуд двух соседних колебаний:
 , (5)
, (5)
где  – амплитуда в момент времени t,
– амплитуда в момент времени t, 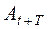 – амплитуда через один период
– амплитуда через один период  .
.
Установим связь между логарифмическим декрементом и коэффициентом затухания  ,
, 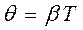 . Используя это соотношение уравнение для амплитуды (4) можно записать как функцию числа совершенных колебаний N. Подставив время
. Используя это соотношение уравнение для амплитуды (4) можно записать как функцию числа совершенных колебаний N. Подставив время  и коэффициент затухания
и коэффициент затухания  , получим
, получим 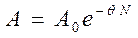 . Отсюда видно, что логарифмический декремент равен величине, обратной числу колебаний за время релаксации.
. Отсюда видно, что логарифмический декремент равен величине, обратной числу колебаний за время релаксации.
 Логарифмический декремент характеризует потери энергии. Полная энергия колебаний равна
Логарифмический декремент характеризует потери энергии. Полная энергия колебаний равна  , или
, или  . Потери энергии за малое число колебаний определим, дифференцируя функцию энергии
. Потери энергии за малое число колебаний определим, дифференцируя функцию энергии  . Примем
. Примем  и получим
и получим  . Логарифмический декремент равен относительным потерям энергии за половину периода.
. Логарифмический декремент равен относительным потерям энергии за половину периода.
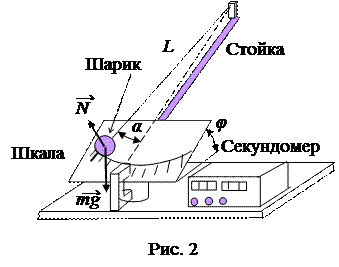
Установка для изучения затухающих колебаний представляет собой шарик, который катается по наклонной плоскости на нити (рис.2). Будем считать, что затухание колебаний обусловлено в основном трением качения шарика по плоскости. Работа силы трения за половину периода (от центра до края и обратно) равна произведению силы трения  на путь, равный двум амплитудам:
на путь, равный двум амплитудам:  . Здесь μ – коэффициент трения качения, α – амплитуда угла поворота, L – длина нити. Потери потенциальной энергии колебаний за половину периода равны
. Здесь μ – коэффициент трения качения, α – амплитуда угла поворота, L – длина нити. Потери потенциальной энергии колебаний за половину периода равны  , где
, где  – высота подъема шарика. Приравняв потери энергии к работе силы трения, получим для коэффициента трения качения
– высота подъема шарика. Приравняв потери энергии к работе силы трения, получим для коэффициента трения качения
 . (6)
. (6)
ВЫПОЛНЕНИЕ РАБОТЫ
1. Установить некоторый угол наклона плоскости φ. Убедиться, что в положении равновесия шарик находится против нуля шкалы. Отвести шарик к краю шкалы. Определить начальную амплитуду α 0. Отпустить шарик. Он начнёт совершать колебания. Измерять амплитуду, не останавливая процесс колебаний, через каждые 5 колебаний не менее пяти раз. Результаты записать в таблицу.
| Номер колебания N | ||||||
| Амплитуда α, рад | ||||||
| ln α | ||||||
| Период Т,с |
2. Определить период колебаний. Включить секундомер в сеть 220 В. Отвести шарик к краю шкалы, отпустить, одновременно нажать кнопку «Пуск» секундомера. Измерить по времени десяти колебаний период  . Выключить секундомер.
. Выключить секундомер.
3. Произвести расчеты. Определить натуральные логарифмы амплитуды. Записать в таблицу.
 4. Построить график зависимости логарифма амплитуды от числа совершенных колебаний N (рис. 2). Размер графика не менее половины страницы. На осях координат нанести равномерный масштаб. Так как зависимость логарифма амплитуды от числа колебаний является, линейной:
4. Построить график зависимости логарифма амплитуды от числа совершенных колебаний N (рис. 2). Размер графика не менее половины страницы. На осях координат нанести равномерный масштаб. Так как зависимость логарифма амплитуды от числа колебаний является, линейной:  , то около точек следует провести прямую линию.
, то около точек следует провести прямую линию.
5. Определить среднее значение логарифмического декремента как углового коэффициента линии. Для этого на экспериментальной линии как на гипотенузе построить прямоугольный треугольник. Среднее значение логарифмического декремента будет равно отношению катетов (рис. 3):
 . (7)
. (7)
6. Определить среднее значение коэффициента затухания и времени релаксации
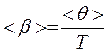 ;
;  . (8)
. (8)
7. Определить по формуле (6) среднее значение коэффициента трения качения по рассчитанному значению логарифмического декремента для наибольшего отклонения шарика α 0.
8. Оценить погрешность измерения  . Случайную погрешность логарифмического декремента определить графическим методом:
. Случайную погрешность логарифмического декремента определить графическим методом:  , рис. 3.
, рис. 3.
9. Записать результат в виде μ= <μ > ± δμ, Р = 0,9. Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие колебания называются затухающими? Какие силы действуют на маятник, совершающий затухающие колебания?
2. Запишите уравнение второго закона Ньютона для маятника. Какие силы действуют на маятник?
3. Запишите уравнение затухающих колебаний. Изобразите график зависимости координаты тела и амплитуды от времени.
4. Дайте определение и физический смысл параметрам затухания: коэффициенту затухания, логарифмическому декременту, добротности, времени релаксации.
5. Выведите формулу для экспериментального определения коэффициента трения качения.
6. Объясните метод графического определения логарифмического декремента и его случайной погрешности.
Работа 11
Поиск по сайту: