 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ. Адиабатический процесс – это процесс, протекающий в термодинамической системе без теплообмена с окружающей средой
|
Читайте также: |
Адиабатический процесс – это процесс, протекающий в термодинамической системе без теплообмена с окружающей средой. Термодинамической системой является система, содержащая огромное количество частиц. Например газ, число молекул которого сравнимо с числом Авагадро 6,02∙1023 1/моль. Хотя движение каждой частицы подчиняется законам Ньютона, но их так много, что состояние системы характеризуют макроскопическими параметрами, такими как давление P, объем V, температура T.
Согласно первому началу термодинамики, являющемуся законом сохранения энергии в термодинамических процессах, теплота Q, подводимая к системе, расходуется на совершение работы А и на изменение внутренней энергии Δ U
Q = A + D U. (1)
В применении к идеальному газу теплота, подводимая к газу приводит к изменению температуры:  , где n = m/M – количество газа, равное отношению массы к массе одного моля, С − молярная теплоемкость, зависящая от вида процесса. Внутренняя энергия идеального газа − это кинетическая энергия всех молекул, она равна
, где n = m/M – количество газа, равное отношению массы к массе одного моля, С − молярная теплоемкость, зависящая от вида процесса. Внутренняя энергия идеального газа − это кинетическая энергия всех молекул, она равна  , где Cv – молярная теплоемкость при изохорическом нагревании. Работа элементарного изменения объема силами давления равна произведению давления на изменение объема: dA = PdV.
, где Cv – молярная теплоемкость при изохорическом нагревании. Работа элементарного изменения объема силами давления равна произведению давления на изменение объема: dA = PdV.
Для адиабатического процесса, происходящего без теплообмена (Q = 0), работа совершается за счет изменения внутренней энергии, A = − D U. При адиабатическом расширении работа газа положительна, поэтому внутренняя энергия и температура понижаются. При сжатии – наоборот. Все быстро протекающие процессы можно достаточно точно считать адиабатическими.
Выведем уравнениеадиабатического процесса идеального газа. Для этого применим уравнение первого начала термодинамики для элементарного адиабатического процесса dA= − dU, котороепринимает вид РdV =−n СvdT. Применим еще одно уравнение, полученное дифференцированием уравнения Менделеева – Клапейрона (PV=νRT): PdV +VdP =nR dT. Исключая один из параметров, например, температуру, получим соотношение для двух других параметров  . Интегрируя и потенцируя, получим уравнение адиабаты через давление и объем: P V g = const. Аналогично для других пар параметров:
. Интегрируя и потенцируя, получим уравнение адиабаты через давление и объем: P V g = const. Аналогично для других пар параметров:
T V g -1 = const, P g -1 T--g = const. (2)
Здесь  – показатель адиабаты, равный отношению теплоемкостей газа при изобарическом и изохорическом нагревании. Получим формулу для показателя адиабаты в молекулярно-кинетической теории. Молярная теплоемкость по определению это количество теплоты, необходимое для нагревания одного моль вещества на один Кельвин
– показатель адиабаты, равный отношению теплоемкостей газа при изобарическом и изохорическом нагревании. Получим формулу для показателя адиабаты в молекулярно-кинетической теории. Молярная теплоемкость по определению это количество теплоты, необходимое для нагревания одного моль вещества на один Кельвин  . При изохорическом нагревании теплота расходуется на повышение внутренней энергии
. При изохорическом нагревании теплота расходуется на повышение внутренней энергии  . Подставив теплоту, получим
. Подставив теплоту, получим  . Тогда показатель адиабаты может быть определен теоретически по формуле
. Тогда показатель адиабаты может быть определен теоретически по формуле
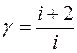 . (3)
. (3)
Здесь i – число степеней свободы молекул газа. Это число координат, достаточное для определения положения молекулы в пространстве или число составляющих компонентов энергии молекулы. Например, для одноатомной молекулы кинетическая энергия может быть представлена как сумма трех компонентов энергии, соответствующих движению вдоль трех осей координат, i = 3. Для жесткой двухатомной молекулы следует добавить еще два компонента энергии вращательного движения, так как энергия вращения относительно третьей оси, проходящей через атомы, отсутствует. Итак, для двухатомных молекул i = 5. Для воздуха как для двухатомного газа теоретическое значение показателя адиабаты будет равно g = 1,4.
Показатель адиабаты можно определить экспериментально методом Клемана – Дезорма. В баллон нагнетают воздух, сжимая до некоторого давления Р 1, немного больше атмосферного. При сжатии воздух несколько нагревается. После установления теплового равновесия баллон на короткое время открывают. В этом процессе расширения 1–2 давление падает до атмосферного Р 2 =Ратм, а исследуемая масса газа, которая до этого занимала часть объема баллона V 1, расширяется, занимая весь баллон V 2 (рис.1). Процесс расширения воздуха (1−2) происходит достаточно быстро, его можно считать адиабатическим, происходящим по уравнению (2)
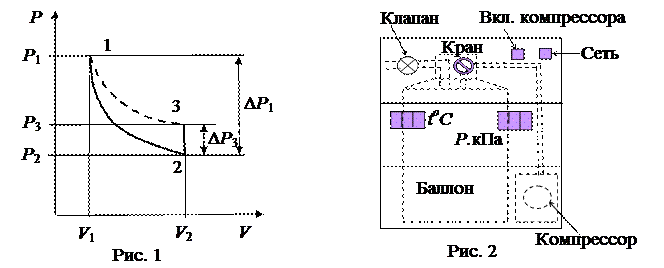
 . (4)
. (4)
В адиабатическом процессе расширения воздух охлаждается. После закрытия клапана охлажденный воздух в баллоне через стенки баллона нагревается до температуры лаборатории Т 3 = Т 1. Это изохорический процесс 2–3
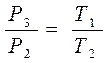 . (5)
. (5)
Решая совместно уравнения (4) и (5), исключая температуры, получим уравнение, связывающее давления:  , из которого следует определить показатель адиабаты γ. Датчик давления измеряет не абсолютное давление, которое записано в уравнениях процессов, а избыточное над атмосферным давлением. То есть Р 1 = Δ Р 1+ Р 2, и Р 3 =Δ Р 3+ Р 2. Переходя к избыточным давлениям, получим
, из которого следует определить показатель адиабаты γ. Датчик давления измеряет не абсолютное давление, которое записано в уравнениях процессов, а избыточное над атмосферным давлением. То есть Р 1 = Δ Р 1+ Р 2, и Р 3 =Δ Р 3+ Р 2. Переходя к избыточным давлениям, получим 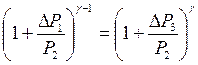 . Избыточные давления невелики по сравнению с атмосферным давлением Р 2. Разложим члены уравнения в ряд по соотношению
. Избыточные давления невелики по сравнению с атмосферным давлением Р 2. Разложим члены уравнения в ряд по соотношению  . После сокращения на Р 2 получим для показателя адиабаты расчетную формулу
. После сокращения на Р 2 получим для показателя адиабаты расчетную формулу
 . (6)
. (6)
Лабораторнаяустановка (рис.2) состоит из стеклянного баллона, который сообщается с атмосферой через клапан «Атмосфера». Воздух накачивается в баллон компрессором при открытом кране «К». После накачивания, во избежание утечки воздуха, кран закрывают.
ВЫПОЛНЕНИЕ РАБОТЫ
1. Включить установку в сеть 220 В.
Открыть кран баллона. Включить компрессор, накачать воздух до избыточного давления в диапазоне 4 –11 кПа. Закрыть кран баллона. Выждать 1,5 –2 мин, записать величину давления Δ Р 1 в таблицу.
| Δ Р 1, кПа | |||||
| Δ Р 3, кПа | |||||
| γ |
2. Повернуть клапан «Атмосфера» до щелчка, клапан откроется и захлопнется. Произойдет адиабатический сброс воздуха с понижением температуры. Следить за повышением давления в баллоне по мере нагрева. Измерить наивысшее давление Δ Р 3 после установления теплового равновесия. Записать в таблицу.
Повторить опыт не менее пяти раз, изменяя исходное давление в диапазоне 3–11 кПа.
Выключить установку.
3. Произвести расчеты. Определить показатель адиабаты в каждом опыте по формуле (6). Записать в таблицу. Определить среднее значение показателя адиабаты < γ >
4. Оценить случайную погрешность измерения по формуле для прямых измерений
 . (7)
. (7)
5. Записать результат в виде: g = < g > ± dg. Р = 0,9. Сравнить результат с теоретическим значением показателя адиабаты двухатомного газа g теор = 1,4.
Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение адиабатического процесса. Запишите первое начало термодинамики для адиабатического процесса. Объясните изменение температуры газа при адиабатических процессах сжатия и расширения.
2. Выведите уравнение адиабатического процесса для параметров давление – объем.
3. Выведите уравнение адиабатического процесса для параметров давление – температура.
4. Дайте определение числа степеней свободы молекул. Как зависит внутренняя энергия идеального газа от вида молекул?
5. Как осуществляются процессы с воздухом в цикле Клемана – Дезорма, как изменяются давления и температуры в процессах?
6. Выведите расчетную формулу для экспериментального определения показателя адиабаты.
СОДЕРЖАНИЕ
Вводное занятие................................................................................................... 3
Работа 1. Изучение удара тел..................................................................... 13
Работа 2. Определение скорости пули баллистическим методом.............. 18
Работа 3. Исследование движения тел в поле тяжести............................... 22
Работа 4. Изучение динамики вращательного движения.......................... 27
Работа 5. Определение скорости пули крутильным маятником................ 32
Работа 6. Определение момента инерции тел............................................. 37
Работа 7. Изучение прецессии гироскопа............................................... 42
Работа 8. Изучение плоского движения при качении тел........................... 47
Работа 9. Изучение плоского движения маятника Максвелла.................. 52
Работа 10. Изучение затухающих колебаний............................................... 57
Работа 11. Изучение вынужденных колебаний............................................ 62
Работа 12. Изучение сложения колебаний................................................... 67
Работа 13. Определение момента инерции физического маятника............. 71
Работа 14. Определение скорости звука в воздухе....................................... 76
Работа 15. Определение теплоемкости воздуха............................................ 81
Работа 16. Определение показателя адиабаты............................................ 86
Поиск по сайту: