Основы теории удара

Ударом в механике называется кратковременное взаимодействие тел, в результате которого резко изменяются их скорости. При таких взаимодействиях возникают столь большие силы, что действием всех можно пренебречь.

Примерами ударов являются:

- удары по мячу, шайбе. В данном случае происходит быстрое, изменение скорости по величине и направлению. Подобные удары с последующим отскоком часто встречаются в перемещающих спортивных движениях;

- приземление после прыжков и соскоков (скорость тела спортсмена резко снижается до нуля). Особенно целесообразно рассматривать приземление как удар, если оно происходит на выпрямленные ноги или связано с падением;

- вылет стрелы из лука, акробата в цирке с подкидной доски и т.п. Здесь скорость до начала взаимодействия равна нулю, а затем резко возрастает.

Изменение ударных сил во времени происходит примерно так. Сначала сила быстро возрастает до наибольшего значения, а затем падает до нуля. Максимальное ее значение может быть очень большим. Однако основной мерой ударного взаимодействия является не сила, а ударный импульс, численно равный заштрихованной площади под кривой F (t). Он может быть вычислен как интеграл:

где S – ударный импульс, t ₁ и t ₂ – время начала и конца удара, F(t) – зависимость ударной силы F от времени t.

За время удара скорость тела, например мяча, изменяется на определенную величину. Это изменение прямо пропорционально ударному импульсу и обратно пропорционально массе тела. Другими словами, ударный импульс равен изменению количества движения тела.

Последовательность механических явлений при ударе такова: сначала происходит деформация тел, при этом кинетическая энергия движения переходит в потенциальную энергию упругой деформации, затем потенциальная энергия переходит в кинетическую. В зависимости от того, какая часть потенциальной энергии переходит в кинетическую, а какая рассеивается в виде тепла, различают три вида удара:

1. Вполне упругий удар – вся механическая энергия сохраняется. Таких ударов в природе нет (всегда часть механической энергии при ударе переходит в тепло). Однако в некоторых случаях удары, например удар бильярдных шаров, близки к вполне упругому удару.

2. Неупругий удар – энергия деформации полностью переходит в тепло. Пример: приземление в прыжках и соскоках, удар шарика из пластилина в стену и т. п. При неупругом ударе скорости взаимодействующих тел после удара равны (тела объединяются).

3. Не вполне упругий удар — лишь часть энергии упругой деформации переходит в кинетическую энергию движения.

Ньютон предложил характеризовать не вполне упругий удар гак называемым коэффициентом восстановления. Он равен отношению скоростей взаимодействующих тел после и до удара. Коэффициент восстановления можно измерить так: сбросить мяч на жесткую горизонтальную поверхность, измерить высоту падения мяча (h _п) и высоту, на которую он отскакивает (h _о). Коэффициент восстановления равен:

Коэффициент восстановления зависит от упругих свойств соударяемых тел. Например, он будет различен при ударе теннисного мяча о разные грунты и ракетки разных типов и качества. Зависит коэффициент восстановления и от скорости ударного взаимодействия:

с увеличением скорости он уменьшается. Например, по международным стандартам теннисный мяч, сброшенный на твердую поверхность с высоты 2 м 54 см (100 дюймов), должен отскакивать на высоту 1,35-1,47 м (коэффициент восстановления 0,73-0,76). Но если его сбросить, скажем, с высоты в 20 раз большей, то даже без сопротивления воздуха отскок возрастет меньше чем в 20 раз.

В зависимости от направления движения мяча до удара различают прямой и косой удары; в зависимости от направления ударного импульса - центральный и касательный удары.

При прямом ударе направление полета мяча до удара перпендикулярно к плоскости ударяющего тела или преграды. Пример: падение мяча сверху на горизонтальную поверхность. В этом случае мяч после отскока летит в обратном направлении.

При косом ударе угол сближения (рис.) отличен от нуля. При идеальном упругом ударе углы сближения и отскока равны. При реальных (не вполне упругих) ударах угол отскока больше угла сближения, а скорость после отскока от неподвижной преграды меньше, чем до удара.

Центральный удар характеризуется тем, что ударный импульс проходит через ЦМ мяча. В этом случае мяч летит не вращаясь. При касательном ударе ударный импульс не проходит через ЦМ мяча – мяч после такого удара летит с вращением. Как уже отмечалось, вращение мяча изменяет траекторию его полета. Изменяет оно также отскок мяча. Например, в настольном теннисе поступательная скорость крученого мяча (шарика) после отскока нередко выше, чем до соприкосновения со столом: часть кинетической энергии вращения переходит в энергию поступательного движения.

При центральном ударе двух упругих тел (например, двух бильярдных шаров) количество движения в системе этих тел остается постоянным: m₁v ₁+ m ₂ v ₂= m ₁ и ₁ +m ₂ u ₂ = const. где mт ₁ и m ₂ – массы первого и второго тела, v ₁ и v ₂ – их скорости до удара; и u ₁ и и ₂ — их скорости после удара.

Если скорость одного из тел до удара равна нулю, то после удара она станет:

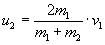
Из формулы видно, что скорость после удара будет тем больше, чем больше скорость и масса ударяющего тела (ударная масса). В более сложных случаях (нецентральный и не вполне упругий удар) картина сложнее, однако и в них скорость после удара будет тем выше, чем больше ударная масса и скорость тела, наносящего удар.

Поиск по сайту: