 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Глава 6. Транспортные задачи по перевозке неоднородного взаимозаменяемого груза
Пусть имеется два поставщика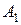 
и 
и 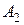два потребителя 
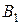и 
. Обозначим через 
и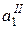 
ресурсы первого поставщика по I и II-у сорту груза соответственно. Аналогично для второго поставщика – 
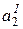и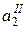 
. Таким образом, в дальнейшем будем рассматривать как бы четыре поставщика с ресурсами 
.
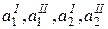Потребности у каждого потребителя могут быть двух видов:
1) потребности только на I-й сорт груза 
;
2) потребности только на II-й сорт груза 
;
В дальнейшем вместо каждого из потребителей В1 и В2 будем рассматривать два потребителя с потребностями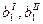 
, 
.
характеризует затраты на перевозку 1 ед. груза из пункта 
в пункт 
. Коэффициенты затрат не зависят от сорта перевозимого груза, а определяются только тем, откуда и куда он перевозится. Известно, что р ед. груза I-го сорта могут быть заменены q единицами II-го сорта. Тогда данные задачи можно выразить в единицах груза первого сорта или второго при помощи коэффициента взаимозаменяемости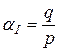 
(в I-й сорт) или 
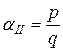(во II-й сорт).
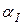показывает, сколько единиц груза I сорта могут заменить одну единицу груза II-го сорта. Аналогичный смысл имеет коэффициент 
.
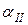Все задачи можно представить в однородном условном грузе в таблице.
Получим задачу с запретами.
Условие баланса 
.
Этого условия недостаточно для разрешимости задачи.
Очевидно, запасы грузов I и II сорта должны быть не меньше потребностей в этих сортах
.
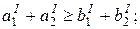
Пример. Найти оптимальный план перевозок угля двух сортов (I – бурый уголь и II – антрацит) из двух складов (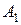 и 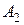) двум потребителям ( 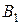и ). Исходные данные задачи приведены в таблице, где указаны запасы угля I сорта (300 и 100 т) и II сорта (100 и 140 т); потребности в угле I сорта (100 и 200 т), II сорта (60 и 40 т) и взаимозаменяемые потребности (220 и 90 т) в единицах I сорта. Известно, что при удовлетворении взаимозаменяемых потребностей три единицы I сорта можно заменить двумя единицами II сорта. Следовательно,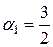 
. В таблице указаны удельные транспортные затраты 
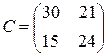, которые могут приниматься пропорциональными расстояниям между соответствующими поставщиками и потребителями (без учета тарифов на перевозки)
Исходные данные задачи
 bj
ai
| B1 | B2 | |||||
| 220(I) | 90(I) | ||||||
| A1 | |||||||
| A2 | |||||||
Пересчитаем данные таблицы в единицах I сорта (бурый уголь) с помощью коэффициента взаимозаменяемости 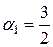. Получаем таблицу
В задаче выполняется условие баланса
.
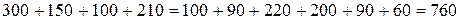Кроме того, выполняются условия удовлетворения потребностей в определенных сортах груза
; 
.
Следовательно, задача разрешима. Решаем полученную задачу с запретами, получаем условно-оптимальный план
Условно-оптимальный план задачи
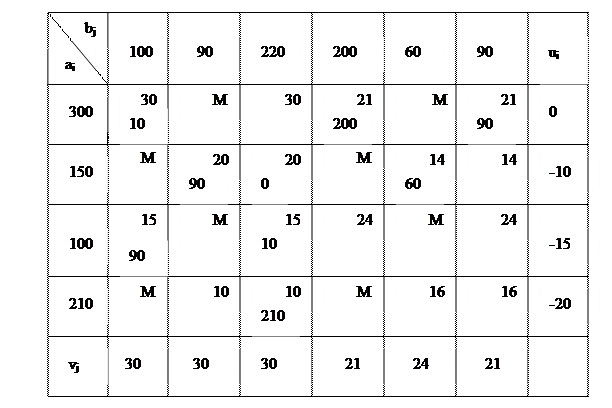
Полученный оптимальный план не единственный, т.к.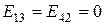 
.
Пересчитаем элементы второй и четвертой строки, разделив их на 
, получаем окончательно оптимальное решение, выраженное уже не в условных, а реальных единицах:
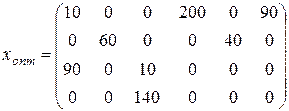
и 
.
Поиск по сайту: