АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Глава 4. Транспортные задачи по критерию времени

Читайте также:
  1. I Психологические принципы, задачи и функции социальной работы
  2. I. 1.1. Пример разработки модели задачи технического контроля
  3. I. 1.2. Общая постановка задачи линейного программирования
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  6. I. ГЛАВА ПАРНЫХ СТРОФ
  7. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  8. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  9. I. Россия в период правления Бориса Годунова (1598-1605). Начало Смутного времени.
  10. I. Россия в период правления Бориса Годунова (1598-1605). Начало Смутного времени.
  11. I. Ситуационные задачи и тестовые задания.
  12. I. Цель и задачи дисциплины

 

Необходимость решения таких задач обусловлена аварийными поставками, при перевозках скоропортящегося груза, обеспечении сырьем бесперебойных производств и при других обстоятельствах.

Задача состоит в следующем.

Заданы m поставщиков и n потребителей с известными ресурсами и потребителями и матрица времени доставки груза 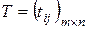. Для задачи выполнено условие баланса 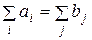. Среди множества планов задачи найти такой, для которого минимизируется время реализации:

.

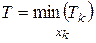Задача

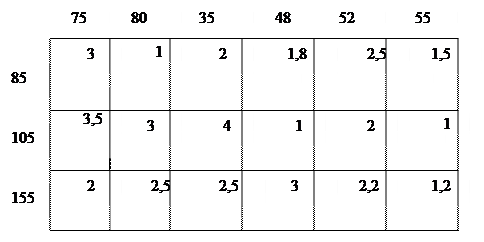
Пусть мощности поставщиков , спрос потребителей и матрица времени представлены в таблице

 
 


ai

75          
        1,8 2,5 1,5
3,5          
  2,5 2,5   2,2 1,2

 

Определить минимальное время реализации плана перевозок.

Решение. Проверяем условие баланса .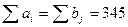

1. Находим первоначальный план по методу минимального элемента матрицы времени

 

 

2. Определяем время реализации плана :

(час).

Наиболее продолжительная перевозка от третьего поставщика к третьему потребителю.

3. Исключаем из рассмотрения клетки с производительностью большей или равной 2,5, чтобы не увеличить продолжительность всего комплекса перевозок при перемещении поставок по контуру.

4. Мы не можем сократить время перевозок, так как не можем построить замкнутый маршрут для клетки (3,3).

руб.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)