Математическая модель задачи

Введем неизвестные величины

Пусть матрица расстояний между городами.

Тогда

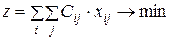; (11.1)

; (11.2)

; (11.3)

– целые. (11.4)

Данная задача относится к числу задач целочисленного программирования. Целевая функция z в (11.1) означает длину маршрута для данного плана переездов. Система ограничений (11.2) обеспечивает построение маршрута, при котором коммивояжер въезжает в каждый город только раз, а система ограничений (11.3) – маршрута, когда он выезжает из каждого города раз. Этих ограничений еще недостаточно для постановки задачи, так как они не исключают решения, в котором вместо простого цикла, проходящего через n вершин, отыскиваются два или более отдельных цикла (подцикла), проходящих через меньшее число вершин. На рис. 7 и 8 приведены связанные и несвязанные маршруты

Рис. 7. Вариант замкнутого Рис. 8. Пример двух замкнутых

маршрута коммивояжера несвязанных маршрутов,

не являющихся решением

задачи коммивояжера

Поэтому для исключения подобных несвязанных маршрутов задача (11.1 – 11.4) должна быть дополнена ограничениями, обеспечивающими связность цикла:

, (11.5)

Условия (11.5) выражают требование цикличности. Переменные и могут принимать произвольные действительные значения.

Введение ограничений (11.5) резко увеличивает размеры модели. Так при n = 50 получается порядка 2500 ограничений. Решение целочисленных задач таких размеров представляет серьезную вычислительную проблему. Между тем во многих практических ситуациях задача коммивояжера является стандартной подзадачей, решение которой должно выполняться многократно. При решении задачи используются различные, хорошо зарекомендовавшие себя эвристические методы и точные методы, в основе которых лежит комбинаторная структура задачи (методы ветвей и границ, динамического программирования).

Задача о коммивояжере в математической постановке эквивалента задаче упорядочения конечного цикла наладочных работ на машине при учете потерь от переналадок.

Рассмотрим решение задачи коммивояжера методом ветвей и границ (алгоритм Литтла).

Этот алгоритм можно сформулировать в виде следующих правил:

1. Находим в каждой строке матрицы минимальный элемент и вычитаем его из всех элементов соответствующей строки. В результате получаем матрицу , приведенную по строкам. Каждый элемент этой матрицы определяется по формуле .

2. Находим минимальный элемент в каждом столбце матрицы : . Матрицу , приведенную по столбцам, получаем с помощью преобразования .

3. Находим константу приведения .

4. Находим степени нулей для приведенной по строкам и столбцам матрицы :

.

Записываем соответствующую степень в правом верхнем углу клетки

5. Выбираем дугу , для которой степень нулевого элемента наибольшая:

.

6. Выходим на две ветви и . Ветвь содержит переход , а – не содержит. Для получения расчетной матрицы вычеркиваем в матрице строку 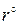и столбец . Заменяем

(симметричный элемент) на , чтобы не допустить образования подцикла.

7. Находим приведенную по строкам и столбцам матрицу и отделяем ее константу приведения h. Тогда нижняя граница ветви определяется по формуле .

8. Для получения расчетной матрицы заменяем элемент на .

9. Находим приведенную по строкам и столбцам матрицу 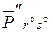и определяем ее константу приведения . Тогда нижняя граница ветви определяется по формуле .

10. Сравниваем нижние границы ветвей. Если , то дальнейшему ветвлению подлежит вариант , в противном случае – вариант и т.д.

11. Если в результате ветвления получаем размерность сокращенной матрицы , то определяем полученный маршрут и его длину (рекорд). В противном случае переходим к шагу 12.

12. Формируем вариант маршрута на базе законченной ветви и определяем его протяженность. Если длина маршрута не превышает нижних границ оборванных ветвей (незаконченных ветвлений), то задача решена. В противном случае развиваем ветви подмножеств с нижней границей, меньшей полученного маршрута до тех пор, пока не получим маршрут с меньшей длиной или не убедимся, что такого не существует.

Пример решения задачи коммивояжера.

Решить задачу для матрицы расстояний в табл. 11

Таблица 11

1. Справа к табл. 11 присоединяем столбец , в котором записываем минимальные элементы строк. Вычитаем из соответствующих элементов матрицы С, получим матрицу, приведенную по строкам (табл. 12):

Таблица 12

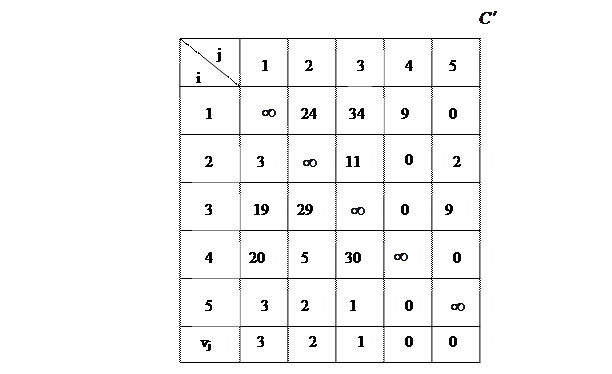
2. Внизу матрицы 12 присоединяем строку , в которой записываем минимальные элементы столбцов. Вычитаем элементы из соответствующих столбцов матрицы . Получим матрицу , приведенную по столбцам (табл. 13)

Таблица 13

3. Находим константу приведения

.

Нижней границей множества всех маршрутов будет число .

4. Находим степени нулей полностью приведенной матрицы (табл. 13), равные сумме минимальных элементов соответствующих строки и столбца. Степени нулей записаны в правых верхних углах клеток, для которых .

5. Определяем максимальную степень нуля. Она равна 10 и соответствует клетке (5,3). Строим дерево ветвлений (рис. 9).

6. Разбиваем множество всех маршрутов на два: и . Матрицу с дугой (5,3) получаем из табл. 13 вычеркиваем пятой строки и третьего столбца. Чтобы не допустить образования подциклов заменяем элемент (3,5) на (табл. 14).

Таблица 14

7. Матрицу маршрутов получим из табл. 13 путем замены элемента на ∞ (табл. 15)

Таблица 15

8. Приводим матрицы и по строкам и столбцам. Константа приведения для матрицы :

.

Нижняя граница множества :

.

9. Находим константу приведения для множества маршрутов : . Следовательно, нижняя граница .

10. Сравниваем нижние границы подмножеств и . Так как , то дальнейшему ветвлению подвергаем множество (табл. 14).

Делаем дополнительное приведение матрицы маршрутов . Приведенная матрица представлена в табл. 16.

Таблица 16

Максимальная степень нуля для клетки (4,2). Претендентом на включение в маршрут будет дуга (4,2). Разбиваем множество на два подмножества и (табл. 17 и 18).

Таблица 17

Таблица 18

Определяем константы приведения для этих матриц , . Следовательно, , . Так как , то дальнейшему ветвлению подлежит множество (табл. 17). Вычисляем степени нулей матрицы . Претендентом на включение в маршрут станет дуга (3,4). Разбиваем множество на два подмножества и (табл. 19 и 20).

Таблица 19

,

Таблица 20

, .

Следовательно, ветвлению нужно подвергнуть множество . Но его матрица имеет размерность . Поэтому в маршрут следует включить дуги (1,5) и (2,1), соответствующие нулевым элементам. Окончательно в маршрут коммивояжера вошли дуги (5,3), (4,2), (3,4), (1,5), (2,1).

Длина маршрута Так как границы оборванных ветвей больше длины контура , то этот контур имеет наименьшую длину.

Если оборванная ветвь имеет меньшую длину маршрута, нужно к ней вернуться и продолжить ветвление.

На рис. 9 приводится дерево ветвлений маршрута коммивояжера.

Рис. 9. Дерево ветвлений маршрута

Вопросы для самопроверки

1. Какова постановка задачи коммивояжера?

2. Как приводится матрица расстояний по строкам и столбцам?

3. Как определяется константа приведения полностью приведенной матрицы?

4. Как определяется степень нулей матрицы приведенной по строкам и столбцам?

5. В каком случае дуга включается в маршрут коммивояжера?

6. До каких пор снижается порядок матрицы маршрута?

7. Как проверить правильность построения маршрута?

8. Как построить дерево ветвлений?

9. В каком случае необходимо вернуться к оборванной ветви?

Задачи для самостоятельного решения

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Поиск по сайту: