Глава 12. Решение транспортной задачи на персональном компьютере с использованием ППП QM for Windows (Transportation)

Алгоритм решения транспортной задачи разработан для закрытых моделей, для которых выполнено условие баланса. В случае открытой модели в программе предусмотрено приведение к закрытой в автоматическом режиме.

Решение задачи начинается с нахождения первоначального опорного плана перевозок. В программе рассматриваются три метода определения первоначального плана: метод северо-западного угла (Northwest Corner Method), метод минимальной стоимости (Minimum Cost Method), приближенный метод Вогеля (Vogel’s Approximation Method), и если при выборе метода указать процедуру «Any Starting Method», то в автоматическом режиме выбирается лучший из трех перечисленных с точки зрения целевой функции.

Далее задача решается методом потенциалов. Характеристики свободных клеток не зависят от того, на каком уровне зафиксирована одна из переменных или , поэтому в отчетах о решении задачи указываются только характеристики.

Транспортная задача имеет команду «Step», дающую пошаговый процесс решения от итерации к итерации. Если задача имеет не единственное оптимальное решение, то все базисные оптимальные решения можно получить, используя только эту команду. Если задачу решить с помощью команды «Solve», то в отчете о решении будет указано последнее оптимальное решение.

Покажем решение задачи с использованием рассматриваемой программы. В диалоговом окне для создания нового файла необходимо, кроме заголовка (Title), указать число источников (поставщиков) (Number of Sources) и число потребителей (Number of Destinations). После ввода этой информации необходимо заполнить появившуюся таблицу исходных данных задачи. В клетки таблицы вносим данные тарифы , в последнюю строку (DEMAND) заносим спрос потребителей, а в последний столбец (SUPPLY) – мощность поставщиков.

Пусть решается задача

;

; .

Рис. 10. Окно исходных данных ТЗ

здесь щелкнули по стрелке вниз в позиции Starting method – начальный метод, чтобы показать возможность выбора метода нахождения начального решения (на рис. 12. выбран метод минимальной стоимости). Решив задачу, можно вывести на экран и напечатать следующие окна

Рис. 11. Список окон отчетов о решении ТЗ

Последовательно они содержат информацию:

– перевозка груза;

– приростная стоимость;

– таблица конечного решения;

– итерация;

– перевозки со стоимостями;

– перечень (список) перевозок.

Приведем и поясним некоторые из них:

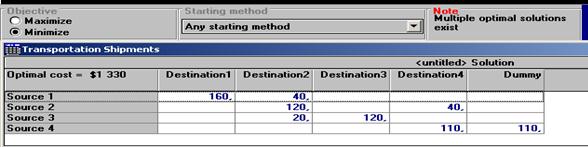
Рис. 12. Окно перевозок груза

В этом окне отражены поставки груза в оптимальном решении транспортной задачи. В правом верхнем углу отчета как примечание отмечено, что задача имеет несколько оптимальных решений и над перечнем источников указано значение целевой функции в оптимальном решении (Optimal cos t = $ 1330), указан метод нахождения начального решения.

Рис. 13. Окно приростных стоимостей в решении ТЗ

В окне приростных стоимостей на рис. 13. отражены характеристики свободных клеток таблицы ТЗ в оптимальном решении. Они показывают, на сколько увеличивается значение целевой функции, если в соответствующую клетку таблицы перераспределить поставку, равную единице. По этой же информации можно судить о числе оптимальных базисных решений – по числу нулевых характеристик (приростных стоимостей). В этом примере имеется две нулевых характеристики.

Остальные окна не требуют дополнительных пояснений. Рассматривалась открытая транспортная задача, т.к. условие баланса не выполнено. , . Алгоритм решения задачи в автоматическом режиме ввел в рассмотрение дополнительного потребителя (последний столбец Dummy) со спросом, равным 110. Поставка от четвертого поставщика дополнительному (фиктивному) потребителю (см. рис. 12.) означает невостребованный груз, оставшийся у четвертого поставщика.

Библиографический список

1. Кузнецов Ю.Н., Кузубов В. И., Волощенко А. Б. Математическое программирование: учеб. пособ. – М.: Высшая школа, 1980.– 380 с.

2. Сакович В. А. Исследований операций. – Минск: Вышейшая школа, 1980.

3. Калихман И. Л. Линейная алгебра и программирование. – М.: Высшая школа, 1967.

4. Бушин П. Я., Захарова В. Н. Математические методы и модели в экономике: учеб. пособ. – Хабаровск: РИЦ ХГАЭП, 1998. – 139 с.

5. Бушин П. Я. Математические модели в управлении: учеб. пособ. – Хабаровск: РИЦ ХГАЭП, 1999. – 100 с.

Учебное издание

Валентина Никитична Захарова

Оптимизация транспортно-экономических связей

Учебное пособие

Редактор Г.С. Одинцова

______________________________________________________________ Подписано в печать 2005г. Формат 60 х 84/16. Бумага писчая.

Печать офсетная. Усл.п.л. 6,0 Уч.-из.л. 4,3 Тираж 250

Заказ №

______________________________________________________________

680042, Хабаровск, ул. Тихоокеанская, 134, ХГАЭП, РИЦ.

Отзыв

на учебное пособие «Оптимизация транспортно-экономических связей»

Учебное пособие составлено доцентом кафедры математики и математических методов в экономике Захаровой В.Н. в соответствии с государственным стандартом по математическим методам и моделям в экономике.

В пособии рассматриваются различные задачи оптимизации транспортно-экономических связей.

Транспортные задачи:

по критерию минимума времени,

с учетом времени и издержек,

с запретами,

с ограничениями по пропускной способности,

по перевозке неоднородного взаимозаменяемого груза,

в сетевой постановке,

двухэтапная производственно-транспортная,

обобщенная λ-задача,

задача оптимального размещения производства,

задача коммивояжера.

В пособии рассмотрен теоретический материал, алгоритмы и примеры решения задач, предложены вопросы для самопроверки, даны задачи для самостоятельного решения, приведено решение транспортной задачи на персональном компьютере с применением ППП QM for Windows.

Учебное пособие предназначено для студентов экономических специальностей всех форм обучения, соответствует требованиям и рекомендуется для внутри вузовского издания.

К.ф.-м.н., ст. научный сотрудник института экономических исследований ДВО РАН

С.А. Ланец

Отзыв

на учебное пособие «Оптимизация транспортно-экономических связей»

Учебное пособие составлено доцентом кафедры математики и математических методов в экономике Захаровой В.Н. в соответствии с государственным стандартом по математическим методам и моделям в экономике.

В пособии рассматриваются различные задачи оптимизации транспортно-экономических связей.

Транспортные задачи:

по критерию минимума времени,

с учетом времени и издержек,

с запретами,

с ограничениями по пропускной способности,

по перевозке неоднородного взаимозаменяемого груза,

в сетевой постановке,

двухэтапная производственно-транспортная,

обобщенная λ-задача,

задача оптимального размещения производства,

задача коммивояжера.

В пособии рассмотрен теоретический материал, алгоритмы и примеры решения задач, предложены вопросы для самопроверки, даны задачи для самостоятельного решения, приведено решение транспортной задачи на персональном компьютере с применением ППП QM for Windows.

Учебное пособие предназначено для студентов экономических специальностей всех форм обучения, соответствует требованиям и рекомендуется для внутри вузовского издания.

К.ф-м.н., доцент кафедры прикладной математики ДВГУПС

Е.Н. Ломакина

Поиск по сайту: