Задание. Найти оптимальное значение реактивной мощности нагрузки (мощности, протекающей в конце ЛЭП), доставляющее минимум потерь активной мощности в ЛЭП

Найти оптимальное значение реактивной мощности нагрузки (мощности, протекающей в конце ЛЭП), доставляющее минимум потерь активной мощности в ЛЭП. Исходные данные:

R = 3,75 Ом;

X = 21 Ом;

B_с = 5,4·10^–4 См;

Нагрузка:

P _н = 360 МВт;

Q _н = 170 Мвар;

Напряжения:

U _ном = 220 кВ;

U ₀ = 232 кВ.

Взаимная проводимость между узлами 0 и 1: . Собственная проводимость узла 1 равна . Емкостная проводимость практически не повлияла на собственную реактивную проводимость

Алгоритм расчета следующий.

1) Задаем исходное приближение Y = (Q ⁽⁰⁾) и рассчитываем для заданного P = –360 и Q ⁽⁰⁾ = –170 установившийся режим (знак минус потому, что задающие мощности – направление «к узлу»). Для этого:

· задаем начальные приближения переменных U ¢ = U _ном и U ¢¢ = 0;

· вычисляем вектор-функцию небалансов мощностей W в точке начальных приближений:

, должно получиться , норма этого вектора равна | W ⁽⁰⁾| = 340,061.

· вычисляем элементы матрицы Якоби ;

· находим невязки для искомых переменных

;

· вычисляем следующие значения искомых переменных:

· снова вычисляем вектор-функцию в полученной точке и, если норма этого вектора достаточно мала, процесс расчета режима заканчивается, в противном случае находится следующее приближение к решению.

В результате трех итераций получаем напряжение:

2) Находится значение целевой функции (потери мощности в ЛЭП).

3) Вычисляется градиент целевой функции.

Для этого вычислим элементы матрицы Якоби и обратной ей матрицы на последней итерации решения уравнений установившегося режима методом Ньютона (см. п.1)

и

Матрица частных производных неявной функции составляющих напряжения по величине реактивной мощности равна

Градиент целевой функции

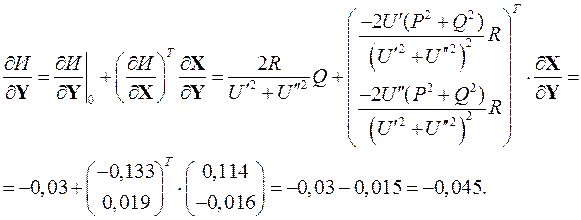
4) Выбирается шаг и находится следующее значение независимой переменной Q ⁽¹⁾. При шаге t = 4620 Q ⁽¹⁾ = 39,09 Мвар.

5) Рассчитывается новый установившийся режим и проверяется норма вектора градиента. Если она достаточно мала, то процесс оптимизации заканчивается, иначе находится новый градиент и делается шаг в направлении убывания целевой функции. После каждого расчета установившегося режима вычисляется значений целевой функции. Каждый раз ее значение должно уменьшаться.

В результате двух итераций по методу Ньютона получаем напряжение:

Градиент целевой функции в новой точке получается равным –2,047·10^–3, что является достаточно малым значением и расчет на этом можно закончить.

Определите, какая реактивная мощность получается в новом приближении и насколько снизились потери активной мощности в линии в результате оптимизации.

Поиск по сайту: