АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Постановка задачи. Найти минимум потерь активной мощности в ЛЭП, рис

Читайте также:
  1. I Психологические принципы, задачи и функции социальной работы
  2. I. 1.1. Пример разработки модели задачи технического контроля
  3. I. 1.2. Общая постановка задачи линейного программирования
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  6. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  7. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  8. I. Ситуационные задачи и тестовые задания.
  9. I. Цель и задачи дисциплины
  10. I.5.3. Подготовка данных для задачи линейного программирования
  11. I.5.4. Решение задачи линейного программирования
  12. I.5.5. Просмотр и анализ результатов решения задачи

Найти минимум потерь активной мощности в ЛЭП, рис. 7, путем оптимального выбора реактивной мощности нагрузки (или выбора мощности компенсирующего устройства).

Целевая функция – это потери мощности в ЛЭП И (Z) (издержки на покрытие потерь в сети) при учете ограничений баланса мощности в узлах ЭЭС W (Z) = 0. Вектор Z является вектором параметров режима ЭЭС, а W (Z) – вектор-функция балансовых ограничений по активной и реактивной мощности.

Выберем в качестве независимой переменной Y = (Q) реактивную мощность в конце ЛЭП. Зависимыми переменными будут составляющие напряжения в узле нагрузки X = (U 1, d 1) или X = (U ¢1, U ¢¢1). Напряжение в начале линии известно по величине и по фазе.

Рис. 7. Линия электропередачи

Сделаем предположение, что ограничения на переменные типа неравенств соблюдаются.

Для простоты обозначим зависимые переменные U ¢1 и U ¢¢1 как U ¢ и U ¢¢.

Выберем выражение для потерь мощности в ЛЭП в виде

Градиент целевой функции вычисляется по выражению:

где

а производные по зависимым переменным U ¢ и U ¢¢

Матрица частных производных неявной функции составляющих напряжения по величине реактивной мощности равна

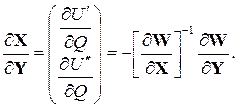
Уравнения установившегося режима, которые используются в данной задаче, записываются как

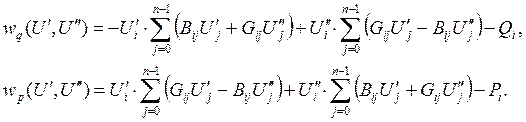
В нашем случае n = 2, а узел с номером 0 является балансирующим базисным узлом, поэтому имеем одно уравнение для P и одно для Q.

По этим двум уравнениям, записанным для узла с номером 1, берутся производные по составляющим напряжений U ¢ и U ¢¢. По соображениям улучшения сходимости итерационного процесса в начале дифференцируем уравнение для Q, а затем по P.

С учетом U0´´ = 0 в результате имеем:

.

Матрица частных производных от вектор-функции W по Q получается простой

Значение переменной Q, полученное на следующем (k + 1-м) шаге спуска к точке минимума, получается по формуле

где t – шаг в направлении убывания целевой функции.

Каждый шаг процесса движения к точке минимума выполняется из точки, параметры режима которой определяют сбалансированный установившийся режим, поэтому перед расчетом следующего значения Q следует рассчитать очередной режим для предыдущего значения Q. Для расчета установившегося режима удобно использовать метод Ньютона.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)