 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Указания
Для пункта 1а.
1) Целевой функцией взять суммарный расход топлива в ЭЭС
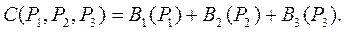
2) Для решения использовать метод неопределенных множителей Лагранжа.
3) Независимыми переменными взять P 1 и P 2. Балансирующим пунктом взять узел 3.
4) Геометрическую интерпретацию поведения целевой функции в области минимума дать в координатах P 1, P 2. Трехмерный график и линии уровня построить в Mathcad с помощью матрицы, которую получить как значения целевой функции c шагом по P 1 и P 2 примерно 4 … 5 МВт.
5) Вычислить целевую функцию в точке минимума.
Для пункта 1б.
1) Целевой функцией взять суммарный расход топлива в ЭЭС
2) Учет изменения потерь мощности в сети выполнить с помощью функций относительных приростов, для этого:
· записать функцию суммарных потерь мощности в сети;
· получить производные по независимым переменным P 1 и P 2.
3) Реактивные мощности и напряжения считать неизменными величинами.
4) Вычислить потери мощности и целевую функцию в точке минимума.
Для пункта 2.
1) Целевой функцией взять суммарный расход топлива в ЭЭС
2) Вместо общего ограничения по балансу мощности в сети использовать уравнения балансов активной и реактивной мощности в независимых узлах сети (во всех узлах кроме балансирующего).
3) Напряжение в балансирующем (базисном) узле задано по величине и по фазе.
4) В качестве уравнений баланса использовать уравнения узловых напряжений, записанные в полярных координатах по напряжениям (U, δ) и в декартовых для остальных переменных:
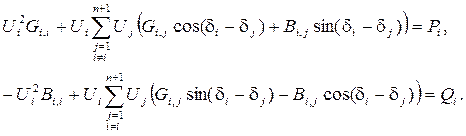
Здесь Gi,j и Bi,j – элементы расширенной матрицы узловых проводимостей.
5) Реактивные мощности считать неизменными величинами.
6) Искомыми величинами являются не только активные мощности станций, но и напряжения на шинах станций 1 и 2 по модулю и фазе.
7) Вычислить потери мощности и целевую функцию в точке минимума. Проверить баланс мощностей по сети в целом.
Для пункта 3.
1) Целевой функцией считать суммарные потери мощности в сети. Формулу для суммарных потерь мощности записать через напряжения узлов сети:

где Ui, Uj и δ i, δ j – напряжения по модулю и фазе по концам k -ой ветви: m – число ветвей в сети; Gk – активная проводимость продольной ветви (вещественная часть обратной величины продольного сопротивления Z k).
2) Найденные в предыдущем пункте значения активных мощностей станций считать неизменными величинами.
3) Для решения оптимизационной задачи распределения реактивной мощности между станциями использовать решающий блок Mathcad с функцией оптимизации minimize.
4) Вычислить потери мощности в точке минимума.
В отчете по лабораторной работе 2 привести все распечатки вычислений и таблицу результатов по нижеприведенной форме (в качестве числовых значений использованы данные контрольного примера по работе):
Таблица
Пример записи результатов расчета
| Параметр | Задача оптимизации | |||
| 1 а | 1 б | |||
| P 1, МВт | 64,75 | 65,01 | 65,16 | 65,16 |
| P 2, МВт | 59,25 | 60,03 | 60,09 | 60,09 |
| P 3, МВт | 75,99 | 78,16 | 77,29 | 76,29 |
| Q 1, Мвар | 3,04 | |||
| Q 2, Мвар | 2,1 | |||
| Q 3, Мвар | –50 | –50 | –50 | |
| U 1, кВ | 247,43 | 239,66 | ||
| U 2, кВ | 246,36 | 238,62 | ||
| δ1, рад | 0,035 | 0,047 | ||
| δ2, рад | 0,024 | 0,035 | ||
| B, тут/МВт ч | ||||
| Δ P, МВт | – | 3,705 | 2,543 | 1,549 |
При защите лабораторной работы уметь объяснить изменение результатов в различных постановках задачи оптимизации.
Контрольные вопросы
1. Постановка задачи нелинейного программирования.
2. Прямой метод оптимизации
3. Метод неопределенных множителей Лагранжа.
4. Формулировка задачи распределения активной мощности между электростанциями. Принцип равенства относительных приростов.
5. Учет изменения потерь мощности в сети в задаче распределения активной мощности. Удельные приросты потерь в сетях.
6. Формулировка задачи распределения активной мощности между электростанциями с учетом режима напряжений в сети.
7. Формулировка задачи распределения реактивной мощности между источниками.
Поиск по сайту: