АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Пример графического решения задачи линейного программирования

Читайте также:
  1. FAST (Методика быстрого анализа решения)
  2. HMI/SCADA – создание графического интерфейса в SCADА-системе Trace Mode 6 (часть 1).
  3. I Психологические принципы, задачи и функции социальной работы
  4. I. 1.1. Пример разработки модели задачи технического контроля
  5. I. 1.2. Общая постановка задачи линейного программирования
  6. I. 2.1. Графический метод решения задачи ЛП
  7. I. 3.1. Двойственная задача линейного программирования
  8. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  9. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  10. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  11. I. Ситуационные задачи и тестовые задания.
  12. I. Цель и задачи дисциплины

Рассмотрим задачу, записанную в канонической форме.

Найти минимум линейной функции семи переменных

L = x 1 – x 2 + 2 x 3 – x 4 – 3 x 5 + x 6 – 2 x 7.

Уравнения ограничений:

xk ≥ 0 (k = 1,…,7)

Решение. Выберем в качестве свободных переменных, например, x 1 и x 2 и выразим через них остальные (базисные) переменные: x 3, x 4, x 5, x 6, x 7. Из первого уравнения имеем:

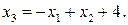
Из третьего

Из четвертого

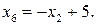
Подставляя x 3 во второе уравнение и x 6 – в последнее и разрешая относительно x 4, x 7, имеем:

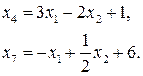
ОДР получается построением прямых, ограничивающих область, в которой xk ≥ 0 (k = 1,…,7).

Подставляя полученные выражения для xk (k = 3,…,7) в целевую функцию, имеем:

Основная прямая L ’ отличается от L отсутствием свободного члена

.

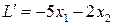Прямая L ’ = 0 проходит через начало координат и для ее построения необходимо взять какую-либо еще точку, лежащую на этой прямой: пусть x 1 = –2, тогда x 2 = 5. При перемещении прямой целевой функции параллельно самой себе функция L будет увеличиваться или уменьшаться. В нашем случае требуется минимизировать целевую функцию. Совершенно ясно, что для положительных x 1 и x 2 уменьшение функции L будет происходить при перемещении прямой в направлении вправо и вверх. Последняя точка ОДР, которая еще будет лежать на прямой целевой функции, находится на пересечении двух прямых x 6 = 0 и x 7 = 0. Координаты этой точки и дают оптимальное решение задачи линейного программирования.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)