АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение задачи распределения активной мощности без учета изменения потерь в сети

Читайте также:
  1. AHD технология: качество 720p/1080p по коаксиалу на 500 метров без задержек и потерь
  2. FSBFRUL (Ф. Правило распределения ассигнований по КЭКР.Заголовки)
  3. I Психологические принципы, задачи и функции социальной работы
  4. I. 1.1. Пример разработки модели задачи технического контроля
  5. I. 1.2. Общая постановка задачи линейного программирования
  6. I. 2.1. Графический метод решения задачи ЛП
  7. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  8. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  9. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  10. I. Изменения капитала
  11. I. Оценка изменения величины и структуры имущества предприятия в увязке с источниками финансирования.
  12. I. Решение логических задач средствами алгебры логики

Условие оптимальности для станций, работающих на одинаковом топливе (одинаковой цене за тонну условного топлива) состоит в равенстве относительных приростов станций. Если считать, что суммарные потери мощности Δ P Σ и суммарная мощность нагрузки постоянны, т.е. не зависит от изменения мощностей станций, то условие оптимальности:

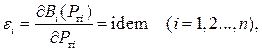
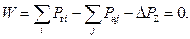
Пример

Найти оптимальную загрузку для двух параллельно работающих ТЭС. Схема содержит две станции (узлы 1 и 2) и одну нагрузку, рис.2.

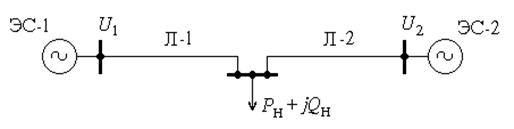
Рис. 2. Схема ЭЭС

Исходные данные: номинальное напряжение сети 220 кВ, нагрузка S н = P н + jQ н = 100 + j 60 МВ·А.

Расходные характеристики станций:

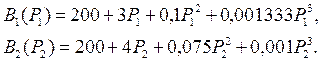
Решение

Найдем характеристики относительных приростов станций.

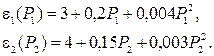
Условие оптимальности:

или

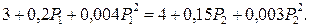
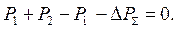
Для простоты примем потери мощности равными нулю, тогда

Подставим P 2 в уравнение равенства относительных приростов и получим уравнение с одним неизвестным P 1

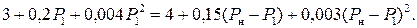
После приведения подобных членов и подстановки P н= 100 МВт, получим квадратное уравнение:

решение которого дает P 1 = 46,177 МВт, после чего находим P 2 = 100 – 46,177 = 53,823 МВт.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)