АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение задачи распределения активной мощности c учетом изменения потерь в сети

Читайте также:
  1. AHD технология: качество 720p/1080p по коаксиалу на 500 метров без задержек и потерь
  2. FSBFRUL (Ф. Правило распределения ассигнований по КЭКР.Заголовки)
  3. I Психологические принципы, задачи и функции социальной работы
  4. I. 1.1. Пример разработки модели задачи технического контроля
  5. I. 1.2. Общая постановка задачи линейного программирования
  6. I. 2.1. Графический метод решения задачи ЛП
  7. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  8. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  9. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  10. I. Изменения капитала
  11. I. Определение основной и дополнительной зарплаты работников ведется с учетом рабочих, предусмотренных технологической картой.
  12. I. Оценка изменения величины и структуры имущества предприятия в увязке с источниками финансирования.

Изменение активных мощностей станций для достижения оптимального режима влияет на потери в сети. Так как потери зависят от мощностей станций, то требуется ввести балансирующий узел, которым является одна из станций ЭЭС. Условие оптимальности для этого случая записывается следующим образом

а для балансирующей станции с номером n:

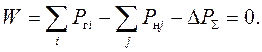
Условие оптимальности для балансирующей станции отличается от условий оптимальности остальных станций, поскольку полагаем, что потери мощности зависят только от мощности всех станций, кроме балансирующей.

Пример

Рис.3. Схема замещения ЭЭС

Рассмотрим условия предыдущего примера, добавив к ним дополнительные данные: U 1 = 220 кВ, U 2 = 242 кВ. R 1 = 2 Ом, R 2 = 5 Ом, Q 1 = 25 Мвар, Q 2 = 30 Мвар. Схема замещения ЭЭС приведена на рис. 3. Балансирующей будем считать вторую станцию.

Потери активной мощности в сети будем определять по выражению:

Условие оптимальности в нашем примере:

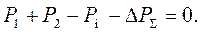и

Аналитическое решение этой системы уравнений затруднительно, поэтому его лучше решить приближенно последовательными приближениями к решению.

Для лучшей эффективности процесса решения выполним нулевое приближение к решению следующим образом.

Вначале найдем решение как в случае без учета изменения потерь в сети, но не с нулевыми потерями, как ранее, а полученными по потокам мощности в сети из предыдущего решения: P 1 = 46,177 МВт и P 2 = 53,823 МВт.

Получим Δ P Σ, затем найдем распределение нагрузки с учетом этих потерь:

.

Далее выполняются несколько итераций, в каждой из которых вычисляются:

1) относительная величина прироста потерь σ;

2) мощность P 1, путем решения уравнения

3) потери мощности Δ P Σ;

4) мощность балансирующей станции

Процесс вычислений заканчивается, когда мощности станций перестанут изменяться сколь либо значительно, например, на величину не более 0,1 МВт.

Решение с такой погрешностью дает: P 1 = 46,3 МВт, P 2 = 54,14 МВт и потери Δ P Σ = 0,442 МВт.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)