АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение задачи распределения активной мощности без учета изменения потерь в сети

Читайте также:
  1. AHD технология: качество 720p/1080p по коаксиалу на 500 метров без задержек и потерь
  2. FSBFRUL (Ф. Правило распределения ассигнований по КЭКР.Заголовки)
  3. I Психологические принципы, задачи и функции социальной работы
  4. I. 1.1. Пример разработки модели задачи технического контроля
  5. I. 1.2. Общая постановка задачи линейного программирования
  6. I. 2.1. Графический метод решения задачи ЛП
  7. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  8. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  9. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  10. I. Изменения капитала
  11. I. Оценка изменения величины и структуры имущества предприятия в увязке с источниками финансирования.
  12. I. Решение логических задач средствами алгебры логики

Пренебрегая потерями, найдем оптимальную загрузку по активной мощности станций для схемы на рис. 4 методом приведенного градиента. Схема содержит три станции (узлы 1, 2 и 3). Нагрузка сосредоточена в узле 2. P н = 200 МВт. Характеристики относительных приростов для этих станций заданы, руб/кВт ч:

Рис. 4. Схема ЭЭС

Решение

Запишем уравнение баланса мощности в системе:

Разделим все переменные данной задачи на вектор Y независимых переменных и на вектор X зависимых. Поскольку система уравнений установившегося режима состоит из одного уравнения, то в векторе X будет всего одна компонента X = (P 2), а вектор Y = (P 1, P 3) (можно принять и любую другую комбинацию).

1) Задаем исходное приближение Y = (P 1, P 3):

P 1 = 50 МВт; P 3 = 50 МВт.

2) Вычисляем P 2 = P н – P 1 – P 3 = 200 – 50 – 50 = 100 МВт.

3) Вычисляем градиент в исходной точке:

где

а из уравнения баланса мощности

Таким образом,

Относительные приросты при текущих мощностях станций равны:

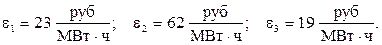
Вектор-градиент grad(И) равен

Мерой сходимости процесса решения выберем величину квадрата нормы вектора-градиента (сумма квадратов элементов вектор-градиента) D2 = 3370.

4) Выбираем пробный шаг t = 0,5 (произвольно) и определяем новые значения переменных:

P 2 = P н – P 1 – P 3 = 200 – 69,5 – 71,5 = 59 МВт.

Им соответствуют относительные приросты:

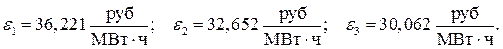
Вектор-градиент и его норма:

Будем продолжать процесс вычислений, двигаясь в направлении текущего антиградиента до тех пор, пока квадрат нормы вектора-градиента не будет меньше 0,1. При этом относительные приросты должны быть равны между собой.

Будем повторять пункт 4, пока не выполнится заданное условие.

Шаг в направлении движения будем выбирать из условия минимума квадрата нормы вектора градиента, зависимость которого от t будем считать параболической. Для интерполяции такой зависимости требуется три точки. Одна из них всегда есть – это квадрат нормы, вычисленный в конце предыдущего шага (t = 0). Две другие можно взять для произвольных значений t. Для простоты выберем точки t = 0,5 и t = 1. Обозначим интерполирующую кривую y = A 0 + A 1 t + A 2 t 2. Минимум этой параболы соответствует точке:

Коэффициенты A 1 и A 2 для выбранных узлов интерполяции находятся по формулам:

где y 1 соответствует t = 0, т.е. для данной итерации y 1 = 19,64; y 2 соответствует t = 0,5 y 2 = 8,27 и y 3 точке t = 1 y 3 = 3,188.

Для полученных значений имеем A 1 =–29,025; A 2 = 12,116 и t = 1,154.

Квадрат нормы вектора градиента уменьшается до 2,851.

Все результаты последующих итераций сведены в таблицу.

Итерация t P 1 P 2 P 3 ε1 ε2 ε3 Δ2
Начальное приближение –              
Пробный шаг 0,5 69,5   71,5 36,22 32,56 30,06 19,64
Второй шаг 1,154 65,28 60,34 74,39 33,1 31,76 33,42 2,851
Третий шаг 0,577 65,46 59,2 75,34 33,23 32,33 32,69 0,423
Четвертый шаг 1,154 64,83 59,41 75,76 32,79 32,58 32,83 0,062

После четвертого шага итерационный процесс можно закончить, так как квадрат нормы практически сведен до нуля и значения относительных приростов стали равны друг другу.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)