АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задачи оптимизации с учетом допусков

Читайте также:
  1. I Психологические принципы, задачи и функции социальной работы
  2. I. 1.1. Пример разработки модели задачи технического контроля
  3. I. 1.2. Общая постановка задачи линейного программирования
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  6. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  7. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  8. I. Определение основной и дополнительной зарплаты работников ведется с учетом рабочих, предусмотренных технологической картой.
  9. I. Ситуационные задачи и тестовые задания.
  10. I. Цель и задачи дисциплины
  11. I.5.3. Подготовка данных для задачи линейного программирования
  12. I.5.4. Решение задачи линейного программирования

 

Содержательную сторону оптимизации с учетом допусков поясняет рис. 7.19, на котором представлены области работоспособности и допусковая в двумерном пространстве управляемых параметров. Если собственно допуски заданы и не относятся к управляемым параметрам, то цель оптимизации – максимальным образом совместить эти области так, чтобы вероятность выхода за пределы области работоспособности была минимальной.

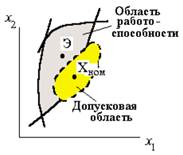
Рисунок 7.19 – Области допусковая и

работоспособности

Решение этой задачи исключительно трудоемко, так как на каждом шаге оптимизации нужно выполнять оценку упомянутой вероятности методами статистического анализа, а для сложных моделей объектов таким методом является метод статистических испытаний. Поэтому на практике подобные задачи решают, принимая те ИЛИ иные допущения.

Например, если допустить, что цель оптимизации достигается при совмещении центров областей работоспособности Э и допусковой Хном, то оптимизация сводится к задаче центрирования, т.е. к определению центра Э. Задачу центрирования обычно решают путем предварительного нормирования управляемых параметров хi с последующим вписыванием гиперкуба с максимально возможными размерами в нормированную область работоспособности.

Примечание. Нормирование проводят таким образом, что допусковая область приобретает форму гиперкуба, получающегося после нормирования.

Очевидно, что решение задачи центрирования позволяет не только оптимизировать номиналь­ные значения проектных параметров, но и их допуски, если последние относятся к управляемым параметрам.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)