АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Пример 2.7. Метод золотого сечения

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. FAST (Методика быстрого анализа решения)
  3. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  4. I. 1.1. Пример разработки модели задачи технического контроля
  5. I. 2.1. Графический метод решения задачи ЛП
  6. I. 3.2. Двойственный симплекс-метод.
  7. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  8. I. Метод рассмотрения остатков от деления.
  9. I. Методические основы
  10. I. Методические основы оценки эффективности инвестиционных проектов
  11. I. Организационно-методический раздел
  12. I. Предмет и метод теоретической экономики

Опять рассмотрим задачу из примера 2.6, в которой требуется

минимизировать f(х) = ( 100— х) 2в интервале 60£ x £150. Для того чтобы перейти к интервалу единичной длины, проведем замену переменной, положив w= (x —60 ) /90. Таким образом, задача принимает следующий вид:

минимизировать f(w)—( 40—90w ) 2

при ограничении 0£ w £1.

Итерация 1. I 1=(0, 1); L 1=l. Проведем два первых вычисления значений функции:

Так как f( w ) 2< f( w1 ) и w2<w1, интервал w≥w1 исключается.

Итерация 2. I 2=(0; 0,618); L 2=0,618=t. Следующее вы­числение значения функции проводится в точке

Так как f( w3 ) > f( w2 ) и w3<w2, интервал w≤w3исключается.

Итерация 3. I 3=(0,236; 0,618), L 3=0,382=t2. Следующее вычисление значения функции проводится в точке, расположенной на расстоянии t ´ (длина полученного интервала) от левой гра­ничной точки интервала, или на расстоянии (1—t) ´ (длина ин­тервала) от правой граничной точки. Таким образом,

Так как f( w4 ) < f( w2 ) и w4>w2, интервал w£w2 исключается.

В результате получен следующий интервал неопределенности: 0,382£ w £0,618 для переменной w, или 94,4£ x £115,6 для перемен­ной х.

Если в процессе поиска проведено шесть вычислений значений функции, то длина результирующего интервала для переменной wравна

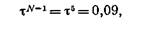
что соответствует интервалу длины 8,1 для переменной х. Для срав­нения напомним, что в аналогичной ситуации метод деления интер­вала пополам привел к получению интервала длины 11,25.

В общем случае если правая и левая граничные точки интервала неопределенности (обозначим их через XR и XL) известны, то ко­ординаты всех последующих пробных точек, получаемых в соответ­ствии с методом золотого сечения, можно вычислить по формулам

w= XR—tn или w = XL + tn

в зависимости от того, какой подынтервал был исключен на преды­дущей итерации — левый или правый. В приведенных выше форму­лах через tn обозначена п- ястепень t, где п — количество вычисле­ний значений функции.

Поиск с помощью метода золотого сечения может быть окончен либо исходя из заданного количества вычислений значений функ­ции (и, следовательно, величины интервала неопределенности), либо по достижении относительной точности искомого значения функции. Наиболее предпочтительным является использование обоих критериев одновременно.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)