АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема 2.3

Читайте также:
  1. I. 4.1. Первая теорема двойственности
  2. S-M-N-теорема, приклади її використання
  3. Б1 1.Системы линейных алгебраических уравнений (СЛУ). Теорема Кроникера-Капелли. Общее решение СЛУ.
  4. Базисный минор и ранг матрицы. Теорема о базисном миноре
  5. Билет 22Понятие евклидова пространства, неравенство Коши-Буняковского. Теорема Кронекера Капелли.
  6. Билет 5 Теорема Безу и следствия из неё. Основная теорема алгебры.
  7. Внешние эффекты (экстерналии). Теорема Коуза.
  8. Внешние эффекты и внешние затраты. Государственная политика в случаях их возникновения. Теорема Коуза.
  9. Внешние эффекты трансакционные издержки. Теорема Коуза
  10. Внешние эффекты, их виды и последствия. Теорема Коуза
  11. Внешние эффекты. Теорема Коуза.
  12. Внешние эффекты. Теорема Коуза.

Пусть функция f унимодальна на замкнутом интервале а ≤ x ≤ b, а ее минимум достигается в точке х*. Рассмотрим точки x 1 и х 2 ,. расположенные в интервале таким образом, что а<x 1 <x 2 <b. Сравнивая значения функции в точках x 1и х 2, можно сделать сле­дующие выводы.

1. Если f(x 1 )>f(x 2 ), то точка минимума f(x) не лежит в интерва­ле (а, х 1 ), т. е. х* Î (х 1, b) (рис. 2.10).

2. Если f(x 1 )<f(x 2 ), то точка минимума не лежит в интервале: (х 2, b), т. е. х*Î (a, x 2 )(см. рис. 2.10).

Доказательство

Рассмотрим случай, когда f(x 1 )>f(x 2 ). Пусть утверждение тео­ремы неверно, т. е. a≤ х*≤ х 1. Поскольку х*— точка минимума, то по определению f(х*)≤f (х) для всех х Î (a, b). Получаем двойное неравенство

f(x*)≤f(x 1 )>f(x 2 ) при x*<x 1 <x 2.

Это неравенство не может выполняться, так как унимодальная функ­ция f (x) должна быть монотонной по обе стороны от точки х*. Таким образом, получено противоречие, доказывающее утверждение тео­ремы. Аналогичные рассуждения справедливы также в случае, когда f(x l )<f(x 2 ).

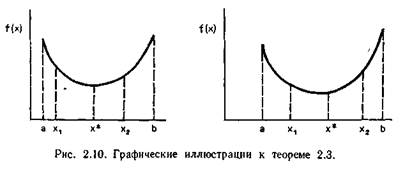
Примечание. Если f(x l )=f(x 2 ), то можно исключить оба крайних интервала (а, х 1 ) и (х 2, b); при этом точка минимума должна распо­лагаться в интервале (x l, x 2).

Согласно теореме 2.3, которую иногда называют правилом ис­ключения интервалов, можно реализовать процедуру поиска, позво­ляющую найти точку оптимума путем последовательного исключе­ния частей исходного ограниченного интервала. Поиск завершается, когда оставшийся подынтервал уменьшается до достаточно малых размеров. Заметим, что правило исключения интервалов устраняет необходимость полного перебора всех допустимых точек. Несом­ненным достоинством поисковых методов такого рода является то, что они основаны лишь на вычислении значений функций. При этом не требуется, чтобы исследуемые функции были дифференцируемы; более того, допустимы случаи, когда функцию нельзя даже записать в аналитическом виде. Единственным требованием является воз­можность определения значений функции f(х) в заданных точках х с помощью прямых расчетов или имитационных экспериментов. Вообще в процессе применения рассматриваемых методов поиска можно выделить два этапа:

этап установления границ интервала, на котором реализуется процедура поиска границ достаточно широкого интервала, содер­жащего точку оптимума;

этап уменьшения интервала, на котором реализуется конечная последовательность преобразований исходного интервала с тем, чтобы уменьшить его длину до заранее установленной величины,


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)