Пример 2.2

Максимизировать f(x)= - x ³+З х ²+9 х+ 10 на интервале -2≤ х ≤4. Имеем

Решая это уравнение, получаем две стационарные точки х= 3и x = -1, которые расположены внутри заданного интервала.

Для того чтобы найти глобальный максимум, вычислим значения f(x) в точках х = 3, - 1, - 2 и 4:

Таким образом, точка х = 3соответствует максимальному значению f на интервале [—2, 4].

Вместо перебора всех стационарных точек и соответствующих значений функции можно воспользоваться специальными процеду­рами, позволяющими найти глобальный оптимум с меньшими за­тратами времени при условии, что функция обладает определенными свойствами. В заключительной части разд. 2.1 было дано определе­ние унимодальной функции, для которой локальный оптимум яв­ляется глобальным. К сожалению, определение унимодальной функ­ции не позволяет непосредственно проверить, является ли функция унимодальной. Однако в теории оптимизации выделяется важный класс унимодальных функций, а именно класс выпуклых и вогнутых функций, которые допускают проверку такого рода. Основные свойства выпуклых и вогнутых функций приведены в приложении Б.

Пример 2.3

Исследуем свойства функции

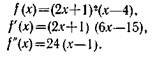
При х ≤1 имеем f"(х) ≤0, и, следовательно, функция является вог­нутой в указанной области. Если же х³ 1то f"(x) ³0, т. е. функ­ция является выпуклой в этой области.

Заметим, что функция имеет две стационарные точки х= -¹/₂ и x = ⁵/₂. Поскольку f"( -¹/₂ ) <0, функция обладает локальным мак­симумом при х= -¹/₂. В точке x = ⁵/₂ вторая производная f"( ⁵/₂ ) >0, и, следовательно, функция достигает в этой точке локального ми­нимума. Если ограничить допустимую область неравенством х ≤1, то f(x) имеет глобальный максимум при х= -¹/₂, так как f(x) — вогнутая функция (в данной области) и х= -¹/₂ — точка локаль­ного максимума. Аналогично если ограничить допустимую область неравенством х³ 1, то f(x) достигает глобального минимума при х = ⁵/₂. Однако если переменная х изменяется на всей действительной оси от - ∞ до + ∞, то функция f(x) не имеет конечного глобального максимума или минимума.

Пример 2.4. Задача управления запасами

Многие фирмы создают запасы производимых товаров для удов­летворения будущего спроса. Среди причин, обусловливающих содержание запасов в определенном объеме, можно отметить нера­циональные потери времени и средств, связанные с их непрерывным пополнением. С другой стороны, пополнение запасов через продол­жительные промежутки времени приводит к образованию чрезмерно больших запасов, которое требует необоснованных капитальных затрат и значительно повышает стоимость хранения запасов. Опре­деление оптимального объема запасов представляет собой классиче­скую задачу оптимизации, для решения которой часто используется так называемая модель определения наиболее экономичного размера заказа.

В рамках этой модели спрос предполагается постоянным и рав­ным l, единиц товара в год. Частое пополнение запасов нецелесооб­разно, так как стоимость выполнения одного заказа составляет К долл. независимо от его размера. Первоначальная стоимость еди­ницы товара равна с долл. Хранение излишних запасов также не­целесообразно, поскольку стоимость хранения единицы товара от­лична от нуля и составляет h долл. в год. Для того чтобы упростить задачу, предположим, что спрос удовлетворяется немедленно (т. е. задолженные заказы отсутствуют), а пополнение осуществляется сразу же, как только запасы иссякают.

Рис. 2.9 иллюстрирует изменение объема запасов с течением времени. В точке А объем запасов равен В; затем объем запасов начинает уменьшаться со скоростью lединиц товара в единицу вре­мени и достигает нулевого значения в точке С. В это время посту­пает новая партия товара, и объем запасов восстанавливается.

Треугольник ABC представляет один цикл управления запасами, который повторяется во времени. Задача заключается в том, чтобы определить оптимальный размер заказа В и продолжительностьинтервала времени между заказами С — А. Обозначим соответ­ствующие переменные через Q и Т.

Поскольку Т есть величина промежутка времени, в течение ко­торого при скорости расходования lистощается запас Q, имеем T=Q/l. Таким образом, задача сводится к нахождению оптималь­ного значения Q. Заметим, что когда Q мало, переменная Т также принимает малое значение. При этом частота заказов велика, что обусловливает большие затраты на выполнение заказов и относи­тельно малые издержки хранения запасов. С другой стороны, нали­чие большого объема запасов (Q велико) приводит к увеличению затрат на хранение запасов и одновременно к снижению издержек, связанных с выполнением заказов на товары. Одна из основных задач управления запасами состоит в определении оптимального значе­ния Q, которому соответствует минимум суммы полных годовых затрат.

Получим аналитическое выражение для функции полных годо­вых затрат (затраты/цикл x количество циклов/год).

Примечание. Затраты на хранение запасов в течение цикла рав­ны затратам на хранение Q /2 единиц товара в течение интервала времени Т.

Таким образом, подлежащая минимизации функция полных затрат есть

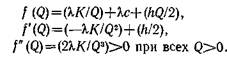
Отсюда следует, что f (Q) — выпуклая функция и если существует положительное значение Q *, такое, что f (Q *)=0, то Q * минимизи­рует f(Q).

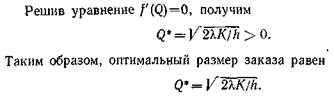
При этом Т* — интервал времени между заказами =т l. Величина Q * известна в теории управления запасами как наиболее экономичный размер заказа.

Поиск по сайту: