 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Доказательство. Утверждение теоремы нетрудно доказать с помощью разложения в ряд Тейлора, представленного равенством (2.1)
|
Читайте также: |
Утверждение теоремы нетрудно доказать с помощью разложения в ряд Тейлора, представленного равенством (2.1). Поскольку порядок первой отличной от нуля производной равен п, формулу (2.1) можно переписать в следующем виде:

Если п — нечетное число, то правая часть (2.6) может принимать как положительные, так и отрицательные значения в зависимости от того, является ли величина e положительной или отрицательной. Это означает, что в зависимости от знака e разность f(x*+ e ) - f (x *) либо положительная, либо отрицательная. Следовательно, функция не достигает в точке х* своего минимального или максимального значения, т. е. х* — точка перегиба.
Далее рассмотрим случай, когда п — четное число. При этом величина en всегда положительная, а знак правой части (2.6) определяется первым слагаемым, если e— достаточно малая величина. Таким образом, если величина (dnf /dxn) ï x=x* положительная, то f(x*+ e )- f (х *)>0 и точка х* соответствует локальному минимуму. Аналогичные рассуждения нетрудно провести также и для локального максимума.
Для того чтобы применить теорему 2.2 к функции f(x)=x 3, график которой изображен на рис. 2.8, вычислим
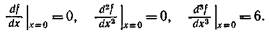
Так как порядок первой отличной от нуля производной равен 3 (нечетное число), точка х= 0является точкой перегиба.
Замечание
Выше предполагалось, что рассматриваемая функция дифференцируема или что ее первая производная существует и непрерывна. Однако если функция не является дифференцируемой во всех точках области определения, то даже необходимое условие наличия оптимума, позволяющее идентифицировать стационарные точки, может не выполняться в точке оптимума. Например, рассмотрим кусочно-линейную функцию

Эта функция непрерывна во всех точках действительной оси, но недифференцируема при х= 2. Функция достигает максимума в точке х= 2, которая не является стационарной в соответствии с данным выше определением.
Пример 2.1
Рассмотрим функцию

определенную на всей действительной оси. Первая производная этой функции равна
df /dx =30 х 5 + 180 х 4+ 330 х 3— 180 х 2 = 30 х 2 (х— 1 ) (х— 2 ) (х— 3 ).
Ясно, что первая производная обращается в нуль в точках х = 0, 1, 2, 3, и, следовательно, эти точки можно классифицировать как стационарные. Вторая производная функции равна

Вычислив значения второй производной в четырех точках х = 0, 1, 2, 3, получим
| x | f(x) | d 2 f /dx 2 |
| 27,5 | ||
| -120 | ||
| 5,5 |
Отсюда следует вывод, что х= 1, 3 — точки локальных минимумов, а х= 2— точка локального максимума. Чтобы идентифицировать точку х= 0, вычислим третью производную

Так как эта производная отлична от нуля и имеет нечетный порядок, то точка х= 0является не точкой оптимума, а точкой перегиба.
Следующий вопрос, к рассмотрению которого мы переходим, связан с определением глобального максимума или минимума функции одной переменной. Поскольку глобальный оптимум является локальным, можно вычислить все локальные оптимумы и выбрать из них наилучший. Алгоритм, основанный на этом простейшем подходе, приводится ниже.
Максимизировать f(x) при ограничении а ≤ x ≤ b,
где а и b — установленные границы изменения значений переменной х.
Так как функция исследуется на заданном интервале, нетрудно заметить, что проверку наличия локального оптимума необходимо проводить не только в стационарных точках, но и в граничных точках интервала.
Шаг 1. Приравнять df/dx= 0и найти все стационарные точки.
Шаг 2. Выбрать все стационарные точки, которые расположены в интервале [ а, b ]. Обозначим эти точки через x 1, х 2,..., х N .
Проверку наличия локального оптимума следует проводить только на множестве указанных точек, дополненном точками а и b.
Шаг 3. Найти наибольшее значение f(x) из множества f(а), f(b), f(x 1 ),..., f(x N ). Это значение соответствует глобальному максимуму.
Примечание. При построении алгоритма мы не пытались классифицировать стационарные точки как точки локального минимума, точки локального максимума или точки перегиба, поскольку для этого требуется вычисление производных высших порядков. Для определения глобального оптимума легче вычислить соответствующие значения функции и выбрать из них максимальное.
Поиск по сайту: