 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Поиск по правильному симплексу
Поиск минимума целевой функции/(Х) по данному методу основан на выборе в качестве пробных точек вершин правильного симплекса. Напомним, что правильным симплексом в Е" называется множество из и+1 равноудаленных друг от друга точек -вершин симплекса. Так, в Е2 правильным симплексом является равносторонний треугольник, в Еъ - тетраэдр.
Из аналитической геометрии известно, что если Х°~ одна из вершин правильного симплекса в Е", то координаты остальных вершин X1,..., ^находятся по формулам
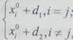
(2.4)
где d, = -
I + n-\); d2 = — =(yJn + \ -l); t - длина ребра.
По известному симплексу можно построить новый симплекс путем отражения какой-либо вершины симметрично относительно центра тяжести А" остальных вершин симплекса. Новая и старая вершины X и Л"* связаны соотношением:
| (2.5) |
л [
В результате получается новый правильный симплекс с тем же ребром и вершинами:
х" =2Xc-Xk,XJ, j = O,...,n,j*k.
Описанная операция отражения в пространстве Ег представлена на рис. 2.1.
V0

|
| х> |
„о Л

Рис. 2.1. Построение нового симплекса в Е2 отражением точки X1:
а - начальный симплекс Х°, Х\ А"2; б- новый симплекс Х°, X1. Х'*\
центр отражения - точка X '= (Х° + Х')/2
На каждой итерации поиска сравниваются значения функции f{x) в вершинах симплекса и выполняется описанная процедура отражения для той вершины, в которой/(л) принимает наибольшее значение. Если в отраженной вершине получается меньшее значение функции, то переходят к новому симплексу. Иначе выполняют еще одну попытку отражения для вершины со следующим по величине значением/(а). Если и она не приводит к уменьшению функции, то сокращают длину ребра и строят новый симплекс с этим ребром. При этом в качестве базовой выбирают ту вершину Х° старого симплекса, в которой функция принимает наименьшее значение. Поиск точки минимума X заканчивают, когда либо ребро симплекса, либо разность между значениями функции в вершинах симплекса становятся достаточно малыми. Опишем один из вариантов алгоритма этого метода.
г
Шаг-0, Задать параметр точности е, выбрать базовую точку Х° и длину ребра t, построить по формуле (2.4) начальный симплекс и вычислить f(X)■
Шаг1. Вычислить значения функции/(А) в вершинах симплекса X',..., X".
Шаг 2. Упорядочить вершины симплекса X,..., Л"1 так,
чтобы f(X°)<...<f{X").
ШагЗ. Проверить условие достижения точности
Если оно выполняется, то перейти к шагу 7, иначе - к шагу 4.
Шаг 4. Найти по формуле (2.4) центр тяжести Х^
вершин Х\Х\..., А""'и выполнить отражение вершины X":
X" =2ХС -X". Если ffx"'^<f(X"-l),TO положить X"'1 = А'""' и перейти к шагу 2, иначе - к шагу 5.
Шаг 5. Найти центр тяжести Xе вершин Х°, X1,..., X" ', X" и выполнить отражение вершины Х"~': X"' = 2Хе -X"'. Если
/|А"1~')</(А"'~|),то положить X"'1 = X" "' и перейти к шагу 2, иначе - к шагу 6.
Шаг 6. Построить новый правильный симплекс с вдвое меньшим ребром, считая базовой вершину А'0, а остальные п вершин находя по формуле X' = [XJ + Xй У2, j -1,..., п, и перейти к шагу 1.
Шаг_7. Завершить вычисления, положив Х'-Х°,/' =/(А"1).
■/ 2.1.2. Поиск но деформируемому многограннику
Практические трудности, возникающие при реализации поиска по правильному симплексу, такие как постоянство величины шага, отсутствие ускорения поиска и трудности при проведении поиска на искривленных поверхностях уровня, привели к необходимости некоторых улучшений метода.
Рассмотрим метод поиска, в котором симплекс может изменять свою форму и уже не остается симплексом. Более подходящим для него оказалось название «деформируемый многогранник».
В методе деформируемого многогранника, как и в предыдущем методе, функция п независимых переменных минимизируется с использованием п+ 1 вершин многогранника. Вершина, в которой значение функции/^ максимально, проектируется через центр тяжести оставшихся вершин. Улучшенные значения функ-цииДА) находятся последовательной заменой точки с максимальным значением/(,¥) на более «хорошие» точки, пока не будет найден минимум/УО-
Итак, пустьX1, Хг,...,Х"*х -вершины многогранника на некотором этапе поиска. Определим точки XhwXL, в которых функция имеет соответственно наибольшее и наименьшее значения:

 Центр тяжести всех вершин, исключая Xh, определим по формуле
Центр тяжести всех вершин, исключая Xh, определим по формуле
X^^-Wx'-X" \. (2.6)
Процедура отыскания вершины, в которой/(Л0 имеет лучшее значение, состоит из четырех операций.
1. Отражение - проектирование точки Xh через центр тяже
сти Х"+г в соответствии с соотношением
Xnri=Xnt2+a(X~2-Xh), (2.7)
где а > 0 - коэффициент отражения: А'"'2 - центр тяжести, вычисляемый по формуле (2.6).
2. Растяжение. Если /(*"*')</(*'), то вектор Х^-Х"*1
растягивается в соответствии с соотношением
X"**=X-*2+y{X"*i-X'*2), (2-8>
где у > 1 - коэффициент растяжения. Если j(X"**)<J[X)• т0 вершина ^заменяется на.Г4 и начинается новый этап поиска
снова с операции отражения. В противном случаев* заменяется на X"" и также осуществляется переход к операции отражения нового этапа.
3. Сжатие. Если f{x"*3) >f(xj)yj * h, то вектор Xй - X"*1 сжимается в соответствии с формулой
X = Х +р(А -X), (2.9)
где (Зе(0;1)-коэффициент сжатия. Вершина Xh заменяется HaX"+i
и выполняется вновь операция отражения на новом этапе поиска.
4. Редукция. Если f(X"1l)>f(x"), то все векторы;Г -*-'■
уменьшаются, например, в 2 раза с отсчетом от XL в соответствии
с формулой
| Далее возвращаемся к операции отражения ния поиска на новом этапе. |
. (2.10)
для продолже-Критерий окончания поиска может быть выбран
| ловия |
в виде ус-
где е > 0 - достаточно малое число.
| Рис. 2.2. Пробные точки Х"*\ X"", Х"*\ X" для перехода к новому многограннику |
Геометрическая иллюстрация описанных процедур для пространства Е1 приведена на рис. 2.2 и 2.3.

IK
Так как величина аб(0;1], то выбор точек Х"*ъ и А'"+3 соответствует отражению; ре(0;1), поэтому выбор точки A""+s соответствует сжатию, а у >1 и выбор точки Х"*л приводит к растяжению симплекса.

|
,-:Y A -
* л" х> '"Y х3' г х'
а б в г
Рис. 2.3. Новые многогранники, полученные в результате процедур отражения (а, б), сжатия (в), растяжения (г)
Деформируемый многогранник в отличие от жесткого симплекса адаптируется в процессе поиска к топографии целевой функции, вытягиваясь вдоль длинных наклонных плоскостей, изменяя направление в изогнутых впадинах и сжимаясь в окрестности минимума.
Влияние параметров алгоритма на эффективность поиска. Проанализируем влияние параметров а, у, р на эффективность
процедуры поиска.
Коэффициент отражения а используется для проектирования вершины с наибольшим значением/(А) через центр тяжести деформируемого многогранника.
Коэффициент у вводится для растяжения вектора поиска в случае, если отражение дает вершину со значением f(X), меньшим, чем наименьшее:шачение/(Л), полученное до отражения.
Коэффициент сжатия (3 используется для уменьшения вектора поиска, если операция отражения не привела к вершине со значением/(ЛО,меньшим, чем второе по величине (после наибольшего) значение/(Л), полученное до отражения.
Таким образом, с помощью операций растяжения или сжатия размеры и форма деформируемого многогранника изменя-
ются так чтобы они удовлетворяли топологии решаемой задачи. После того как это изменение выполнено, размеры многогранника поддерживаются неизменными, пока особенности целевой функции не потребуют применения многогранника другой формы. Это возможно реализовать только при <х=1. Как показывают численные эксперименты, при.решении задачи с col требуется большее количество вычислений функции. При этом параметр а не должен быть много больше единицы, так как деформируемый многогранник легче адаптируется к топологии задачи при меньших значениях а. Кроме того, большое значение а может замедлить сходимость, так как в окрестности минимума размеры многогранника должны уменьшаться. Поэтому значение а= 1 можно выбрать как компромисс.
Влияние на процедуру поиска параметров р и у менее четко выражено. Как показывают результаты решения тестовых задач, можно рекомендовать следующие диапазоны значений для этих параметров: 0,4 < J3 < 0,6; 2 < у < 3. При этом отмечается, что влияние коэффициента р на эффективность поиска заметнее, чем влияние у. При Ре(0;0,4) имеет место преждевременное окончание поиска, а при р > 0,6 требуется выполнить больше шагов для достижения окончательного решения.
^ 2.1.3. Типовой пример
Выполним одну итерацию поиска по методу деформируемого многогранника для задачи минимизации функции f(X) 4(5)2 ()2
) (2)
Поскольку функция зависит от двух переменных, в начале
поиска используется многогранник с тремя вершинами- Xх=( 8- 9)т
ЛГ2=(10;П)т,Л-3=(8;11)т. '
Зададим значения параметров а = 1, у = 2. Вычислим значения функции в них:/(л") = 45;/(х2) = 125;/(Л"3) = 65.
^ Вершиной с наименьшим значением функции оказывается Х'СХг ' ВеРШИН0Й с наибольшим значением функции является X -X. Далее находим центр тяжести вершин, исключая X2.
л =—\л +л) = —|
2V ' 2V20J [\0)
Отражая «худшую» точку Xh относительно найденной X*,
получим точку
9)'
значение функции в которой/(Z5) =13.
Поскольку / [Xs) < f [Xl) = 45,выполняем операцию растяжения, определяя точку
{\0 и значение функции в ней:/(^6) = 8.
Так как /(А'6) < f(xL), заменяем вершину Xй на А""4, полагая X2 = X 6 и тем самым завершая первую итерацию поиска.

|
На рис. 2.4 приведена геометрическая интерпретация поиска по деформируемому многограннику на пяти начальных этапах минимизации функции: /(Х) = 4х2 +х\ -40х, -12х2 +136.
| . 2.4. Траектория поиска по деформируемому многограннику |
Рис
Очевидно линиями уровня функции являются эллипсы. На тс 2 4 и обряжены линии уровня, соответствующие значениям Е™ 2 5 10 20 и 30. Пунктиром выделены многогранники с в ршинами^" U- номер вершины деформируемого многогранника на /-м этапе поиска). Сплошными линиями показана траектория поиска, соединяющая вершины многогранника, соответствующие наименьшим значениям/С*) в каждом из них.
Убедитесь в соответствии графической иллюстрации описанному с помощью формул (2.7) - (2.10) алгоритму.
Порядок выполнения лабораторной работы
1. Кратко описать изучаемые прямые методы безусловной
минимизации функций многих переменных.
2. Выполнить алгоритмическую реализацию описанного ме
тода деформируемого многоугольника.
3. Дать геометрическую иллюстрацию указанной препода
вателем задачи и выполнить вручную две итерации по состав
ленному алгоритму.
4. Провести с использованием компьютерного комплекса
расчеты полученной задачи при различных значениях парамет
ров алгоритма.
5. Проанализировать влияние параметров алгоритма на его
сходимость. Дать геометрическую интерпретацию поиска.
6. Сформулировать вывод о влиянии параметров алгорит
ма на эффективность поиска решения задачи. Содержание рабо
ты отразить в отчете.
Задания для лабораторной работы
1. Минимизировать функцию f(x) = 2xf + r2 -*,*,, исполь
зуя в качестве начального многогранник с вершинами X '=(2- 2)т
л =(3;2,5)', А"=(2;3)т '
2. Минимизировать функцию f(x) = 5х? + 5хг2 + 8*, х2 ис-
3. Минимизировать функцию/(X) = 4.x,2 + х\ -40х, - 12л, +136,
используя в качестве начального многогранник с вершинами
A"=(8;9)T,A-2=(10; 11)Т,ЛГ3=(8; 11)т.
4. Минимизировать функцию f[X) = 2х] + 2х\ - 2х,х, - 14х, -
- \2хг + 29, используя в качестве начального многогранник с вер
шинами Хх= (6;3)Г,Х2=(9; 3)\Х'= (7;4)т.
5. Минимизировать функцию f(X) = x* +4xl -Wjc, -48.x, +169
используя в качестве начального многогранник с вершинами
Xх = (7; 3)т, Х1= (9; 1)т, Xi= (9; 3)т.
6. Минимизировать функцию/(Аг) = х,2 +9x1 -4.x, -18х2 +13,
используя в качестве начального многогранник с вершинами
Xх = (4; Ъ)\Хг= (6; 3)т,^ = (6;4)т.
7. Минимизировать функцию/(-Y) = 9xl2 +х\ -36х, -2х2 +37,
используя в качестве начального многогранник с вершинами
Х' = (5; 3)т,*2=(7; 5)т,^ = (5;5)т.
8. Минимизировать функцию f (X) =\00(х2-х[1)2+ (1-х,)2,
используя в качестве начального многогранник с вершинами
А" = (-1; \)7,Х2=(-0,5; 1)т,Х3=(-1; 2)т.
2.2. Методы покоординатного спуска
Рассмотрим прямые методы решения задачи безусловной минимизации (2.1), использующие вместо итерационных процедур вида (2.3) простейшие вычислительные алгоритмы, основанные на рекуррентной формуле
Xk*l=Xk+akS\ (2.12)
где Sk - направление поиска точки л[ из точки Хк, а положительное число <хк - величина шага в этом направлении.
Способ выбора Sk и о^ будет определять одну из четырех рассматриваемых далее модификаций метода покоординатного спуска.
Поиск по сайту: