 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Алгоритм наилучшей пробы
Л™"" аЛГ°РИ™ 0Тличается от предыдущего тем, что на каж итерации с помощью датчика случайных чисел формируется
где сумма берется только по тем;, 1 <; < s, для которых Y' e R, и по этому направлению делается шаг величиной а.
Если точка А"= Хк+аР\ полу ченная в результате этогооиага принадлежит допустимой области R, то полагают X X
| повторяют |
щей итерации. Если жеХг R, то с новым набором из, реализа-
Построенный таким образом вектор /> называется статистическим градиентом. Такое название связано с тем, что в случае rTe" v = «iJ=ej где е1- единичные координатные векторы, описанный Алгоритм превращается в разностный аналог градиентного метода и направление Рк при Р^О становится направлением антиградиента/(А) функции в точке X.
Величины 5>1,(3>0,а>0 являются параметрами алгоритма, существенно влияющими на качество итерационной процедуры.
Порядок выполнения работы
1. Кратко описать рассмотренные варианты метода случай
ного поиска.
2. Составить рабочие алгоритмы для каждого из них.
3. Выполнить с использованием компьютерного комплекса
расчеты индивидуальной задачи по каждому из трех алгоритмов
при различных значениях их параметров.
4. Провести сравнительный анализ полученных результатов.
Дать графическую иллюстрацию решения задачи по каждому алго
ритму.
5. Сформулировать выводы о влиянии параметров алгорит
мов на сходимость метода и о сравнительной эффективности изу
ченных алгоритмов. Содержание проделанной работы отразить
в отчете.
Задания для лабораторной работы Решить задачи нелинейного программирования:
(= x] -2х2+1>0;
. 9х2 + 27 > 0; g, (X) = -5х2 +16х2 + 80 > 0;
+125 > 0; g2 {X) = -х\ + 2х, + 4х2 + 3 > 0; g3 (X) = х, > 0; g4 (X) =
4. f{X) = x; +9х; -Юх, -18x2+34-»min; gl{X) = -xl -x2 +
+ 5>0;g2{X) = -0,5х,2 + х2 + 4,5>0; g3 (X) = х, >0; g4(А') = х2 >0.
5. / (X) = х; + 4х; - 10х, - 16х2 + 41 -> mm; g, {X) = -х] + 4х,
- х2 + 1 > 0; g2 (X) = -х,2 + 4х, + Зх2 - 3 > 0; g3 {X) = х, > 0; g4 (Z) =
| = -2x,: +4x, |
= х,2 +4.х2 -8.x, -16х2
7. /(Х) = х2+х2-4х,-:
g2 (X) = -xf + х2 > 0; g3 {X) = х, > 0; g4 {X) = х2 > 0.
8. /(X) = х2 + 9х22 - 10-v, - 36х: + 61 -> min; g, (X) = -х,2 + 4х, •
— Ах + 12 > 0' " ' V^ ^v" 4- / V. + Z/ iiU, «,(-"■ / = *l -"' ^Л /
= х2 > 0.
Предполагая, что функции/. (,, m u(
рывно дифференцируемы по совокупности 1^*^
Шить поставленную задачу приближенно г ™
ного метода первого порядка С П°М°ЩЬЮ
4 ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
4.1. Постановка задачи оптимального управления
Рассматривается некоторая техническая система, математической моделью которой является гладкая динамическая система с непрерывным временем:
X = f(t,X(t),u(t)),te[to,tk]; (4.1)
*('.) = *„; (4.2)
где X(t) = (*,«), x2(t),...,xJLt)),u(t) = (M,(0,.... и,(0),/= (fvfv-.f).
Начальное состояние системы {/0, Д;о)} и время перехода tk - t0 считаются заданными, X(tk) - свободно.
Качество управления предлагается оценивать интегральным функционалом
4.2. Градиентный метод решения задачи оптимального управления
4.2.1. Описание градиентного метода в функциональном пространстве
Градиентный метод является одним из эффективнейших численных методов решения задачи оптимального управления. Он состоит в последовательном «улучшении» некоторого произвольно заданного управления, а именно: на каждом этапе улучшения предыдущее управление исправляется в напрвлении наибыстрейшего приближения к искомому оптимальному управлению.
Перейдем к конструированию алгоритма, реализующего данный метод.
Пусть известно некоторое допустимое управление «нулевого приближения» u-u"{t), которому соответствует в силу (4.1), (4.2) фазовая траектория X" (t) и некоторое численное значение функционала /°=/ [и°(')]. вычисленное по формуле (4.3).
Построим новое управление
(4.4)
X{t),u{t))dt. (4.3)
'о
Тогда оптимизация рассматриваемой технической системы сводится к решению следующей задачи оптимального управле-
Для динамической системы (4.1) найти управление „(/),
'el'«.g. переводящее ее m1a™uu^..................... „_.. v J^
| мала. |
где 5w(0 такова, что норма ||5м| = max max
Тогда вариация фазовой траектории, вызванная таким равномерно малым изменением управления, будет подчиняться так называемым уравнениям в вариациях:
™Ж&хЬ)+£-Н')М'лЪ (45)
Л дХ у'ди
= 0. <4-6>
| ледующему результату. |
дних от / = /0 ДО' = '»с введением вспо-
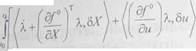 к с
к с
Л = 0. (4.7)
Однако непосредственное варьирование функционала (4.3) дает следующее соотношение:
\ /af°. Л I
(4.8
671^
Добавим к правой части соотношения (4.8) равное нулю выражение (4.7):
5/ = <

Потребуем, чтобы вектор-функция X(t) удовлетворяла следующим условиям:
(4.9)
40 = 0. (4.Ю)
Тогда задача построения согласно формулам (4.4) нового «улучшенного» управления сводится к задаче минимизации функционала:
(4.11)
где Я =j 66
Очевидно, что поправки 5м = (5и (г), 6 ющие минимум 5/в соответствии с (4.11 следующим необходимым условиям:
S1gn8M(,)=slgn|:,v,e[,0,(t]. (413)
Таким образом, «улучшенное» управление u(t)=(u (/) „ (t)..., мг(/)), V?e[>0, /J, найдем по формулам (4.4), задавая достаточно малые абсолютные значения поправок 8и, i = 1,..., г, и определяя их знаки по формулам (4.13).
Следует, однако, отметить, что предложенное правило вычисления поправок 8м(, / = 1,..., г, V (£ [ro, /J, не гарантирует обязательного убывания функционала (4.3) на каждом этапе расчета. Это объясняется невозможностью заранее предполагать, что принятым значениям поправок будет соответствовать значение 5/, близкое к А/. Поэтому на каждом этапе расчета следует находить Д/ = / - /° и в случае, если Л/ > 0, расчет следует повторить при уменьшенных |8м.|, i = 1,..., г.
Поиск по сайту: